Logística/Localização/Localização em redes/Localização em redes em árvore/Localização mediana

Quando se fala em localização mediana o objectivo é encontrar um ponto $\ x^{*}$ que minimiza a soma das distâncias ponderadas entre a nova instalação e os clientes localizados nos nós de uma rede em árvore, $\ v_{i}$. Ao ponto $\ x^{*}$ dá-se o nome de mediana absoluta (Francis, 1992, p. 400-403).

O número de deslocações, o custo de transporte ou o tempo de deslocação por unidade de distância, durante um periodo de tempo, entre o ponto $\ x$ e o vértice $\ v_{i}$ representa-se por $\ w_{i}$, logo, o objectivo é minimizar:

$\ f(x)=w_{1}d\ (x,v_{1})+...+w_{m}d\ (x,v_{m})$

Neste problema, apenas os vértices são considerados como localizações potenciais, em que pelo menos um deles é uma localização óptima ou mediana absoluta e a localização mediana depende dos pesos, $\ w_{i}$, assim como da estrutura da árvore, mas é independente das distâncias entre os nós. Estas distâncias só influenciam o valor de $\ f(x)$.

Algoritmo da Maioria

Este algoritimo é utilizado para determinar o valor da mediana, seguindo os dois passos indicados abaixo:

1. Escolher um nó $\ v_{t}$ com peso $\ w_{t}$ em qualquer um dos extremos da árvore. Se $\ w_{t}$ for maior que $\ W/2$, onde $\ W$ é a soma dos pesos dos nós, esse nó é a mediana, caso contrário executar o passo 2.

2. Designar por $\ v_{a}$ o nó adjacente a $\ v_{t}$. Somar $\ w_{t}$ a $\ w_{a}$, de forma a encontrar o novo peso do nó $\ v_{a}$ e apagar da árvore o arco $\ [v_{t},v_{a}]$, excepto $\ v_{a}$, e voltar ao passo 1.

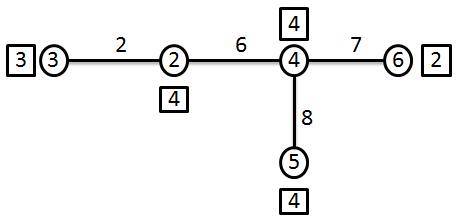
Na Figura 9.12.1.1.1 o peso dos nós está representado nos quadrados, sendo $\ W/2=8,5$.

Figura 9.12.1.1.1 Exemplo de rede em árvore com o peso dos nós dentro dos quadrados

Para encontrar a mediana da árvore representada na Figura 9.12.1.1.1 escolhe-se, por exemplo, $\ v_{1}$.

O peso de $\ v_{1}$ é 2, como $\ 2<W/2$, $\ v_{1}$ não é mediana, segue-se, portanto, para o passo 2, ou seja, adiciona-se o peso de $\ v_{1}$ ao vértice adjacente $\ v_{2}$, eliminando o caminho que ligava $\ v_{1}$ a $\ v_{2}$, dando origem à seguinte rede em árvore (Figura 9.12.1.1.2):

Figura 9.12.1.1.2 $\ v_{2}=v_{1}+v_{2}$

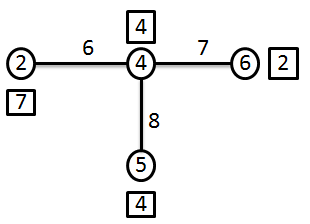
Seguidamente escolhe-se $\ v_{3}$. Como o peso de $\ v_{3}$ é inferior a $\ W/2$, adiciona-se o peso de $\ v_{3}$ ao vértice adjacente $\ v_{2}$, eliminando o caminho que ligava $\ v_{3}$ a $\ v_{2}$. A rede resultante é apresentada na Figura 9.12.1.1.3.

Figura 9.12.1.1.3 $\ v_{2}=v_{3}+v_{2}$

De seguida escolhe-se o vértice $\ v_{2}$. Como $\ w_{2}=7$ é menor que $\ W/2$, volta-se a repetir o passo 2, dando origem a outra árvore, representada na Figura 9.12.1.1.4.

Figura 9.12.1.1.4 $\ v_{4}=v_{2}+v_{4}$

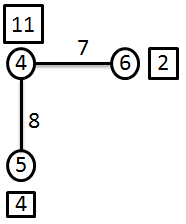
Como $\ w_{4}>W/2$, $\ v_{4}$ é a localização mediana, sendo o valor óptimo da função objectivo dado por:

$\ f(x^{*})=(2\times 11)+(2\times 6)+(3\times 8)+(4\times 8)+(2\times 7)=104$