Discussão:Cálculo (Volume 2)/Geometria tridimensional/Vetores e produtos

Eu diria que há uma certa imprecisão nessa seção. Pelo que eu aprendi, o produto vetorial é definido primeiro a partir do módulo (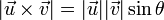$|\vec{u} \times \vec{v}| = |\vec{u}||\vec{v}|\sin\theta$, igual à área do paralelogramo definido pelos dois vetores), pela direção (ortogonal a ambos os vetores) e sentido (dado pela regra da mão direita). É a partir disso que é deduzida a outra expressão para o produto (assumindo uma base ortonormal), $\vec{u} \times \vec{v} = \langle v_y u_z - u_y v_z, v_x u_z - u_x v_z, v_x u_y - u_x v_y \rangle$. Será que não seria mais interessante usar essa definição? ― Eduardo Dobay 00h42min de 26 de Junho de 2007 (UTC)

Você tem razão, quando fala que o produto vetorial é mais didaticamente compreensível quando definido desta forma, de fato a definição assim expressa é mais apropiada para o entendimento do produto. No caso da análise atual, eu não chamaria de imprecisa, é apenas uma maneira mais trabalhosa de chegar ao resultado. Eu sou adepto da análise fundamental, ou seja, utilizo o conceito que deu fundamento ao ente matemático, teoria operatória de matrizes e determinantes, para deduzir o seu significado, por isso costumo usar este tipo de análise... Livros como a série de cálculo de James Stewart também o fazem. Porém, se você acha mais didático fazer a definição a partir do sentido geométrico, pode adaptá-lo. Observe que no caso do produto escalar esta linha também foi usada. --Marcos A. N. de Moura 02h02min de 26 de Junho de 2007 (UTC)

O histórico anterior da página foi arquivado para fins de backup em Discussão:Cálculo (Volume 2)/Geometria tridimensional/Vetores e produtos/Arquivo LQT 1 em 2015-11-03.