Cálculo (Volume 1)/Análise de funções elementares (1)

Wikiversidade - Disciplina: Cálculo I

O estudo das funções deste capítulo refere-se às funções não puramente algébricas, relacionadas a números transcendentais, algumas das quais já conhecemos da matemática elementar, porém é necessário um aprofundamento do tema para o ambiente acadêmico, onde temos que lidar com análises mais detalhadas e complexas.

Logarítmicas

A integral da função algébrica $f(x)=x^{n}$ traz uma indefinição quando $n=-1$:

$\int x^{n}dx={\frac {x^{n+1}}{n+1}};n\neq -1$

A existência desta indefinição nos leva a uma questão: Qual o procedimento para integrar a função: $f(x)={\frac {1}{x}}$? A resposta é dada na análise numérica, calculando a integral pelos métodos de análise algébrica podemos chegar a seguinte conclusão:

$\int _{1}^{x}{\frac {1}{t}}dt=\ln |x|$

A função ln é chamada de logaritmo natural, a sua base é chamada de número de Euler, ele é um logarítmo conseqüente do cálculo da área sob a curva da função $f(x)={\frac {1}{x}}$, que pode ser obtido numericamente usando a integral de Riemann e outras técnicas de cálculo numérico. Aproximações deste número são possíveis utilizando-se técnicas de aproximações sucessivas com o uso de séries, discutidas em Cálculo (Volume 3).

Todos os teoremas para logaritmos, que estão incluidos nos cursos de nível médio, podem ser obtidos a partir da análise do logaritmo natural, também chamado de logaritmo Neperiano.

Teoremas

Vejamos os principais teoremas para os logaritmos:

Nas citações abaixo, consideremos $f(x)=\ln x$,

T36 - Produto

$\ln a\cdot b=\ln a\ +\ \ln b$

Comprovação:

Da definição:

$\int _{1}^{ab}{\frac {1}{u}}du$

$\int _{1}^{a}{\frac {1}{u}}du+\int _{a}^{ab}{\frac {1}{u}}du$

fazendo $u=at,du=adt$ e quando $u=a,t=1$:

$\int _{1}^{a}{\frac {1}{u}}du+\int _{1}^{b}{\frac {1}{at}}adt$

$\int _{1}^{a}{\frac {1}{u}}du+\int _{1}^{b}{\frac {1}{t}}dt$

O que comprova o teorema.

T37 - Razão

$\ln {\frac {a}{b}}=\ln a\ -\ \ln b$

Comprovação:

Sendo $a={\frac {a}{b}}\cdot b$:

$\ln a=\ln {\frac {a}{b}}\cdot b$

$\ln a=\ln {\frac {a}{b}}+\ln b$

logo:

$\ln {\frac {a}{b}}=\ln a-\ln b$

T38 - Potência

$\ln a^{b}=b\cdot \ln a$

Comprovação:

Sendo:

$\ln a^{b}=\ln(a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a\dots )$ -> b vezes, que é:

$\ln a^{b}=\ln a+\ln a+\ln a+\ln a+\ln a+\ln a+\ln a+\ln a\dots )$ -> b vezes, resultando:

$\ln a^{b}=b\cdot \ln a$

Derivadas

Da definição do logarítmo natural e a partir do teorema fundamental do cálculo, podemos deduzir a derivada da função logarítmica natural, ou seja, se $f(x)=\ln x$ que é a integral definida de ${\frac {1}{x}}$, então a derivada é:

${\frac {df(x)}{dx}}={\frac {1}{x}}$

Integrais

Para integração de funções logarítmicas, veja o capítulo de técnicas de integração, para uma completa abordagem do tema.

---

Exponenciais

A função $f(x)=a^{x}$ é chamada de função exponencial na base a, todas as funções exponenciais são introduzidas a partir da definição do logaritmo natural ln x como sua função inversa. As funções exponenciais são estas em que a parte variável é o logaritmo, ou seja:

Se $\log _{a}b=x$

então:

$a^{x}=b$

O que implica $b=f(x)$, tornando-o uma função, na qual podemos atribuir valores a x e obter uma imagem. O número a é chamado base, este número é facilmente identificado nos logaritmos convencionalmente abordados na matemática elementar, mas qual é a base da função $\ln x$ ?

Esta questão nos leva a um novo conceito abordado na próxima seção, o número de Euler.

O número de Euler

A base do logarítmo natural é o número de Euler, simbolizado por: e, ele é obtido pela definição do logaritmo natural, esse número corresponde á área sob a curva da função: $f(x)={\frac {1}{x}}$, quando seu valor é unitário, ou seja:

$\ln e=1$,

mais formalmente:

$\int _{1}^{e}{\frac {1}{x}}dx=1$

O valor deste número pode ser encontrado por aproximação, utilizando-se os métodos de análise de seqûencias e séries, encontrados no livro: Cálculo (Volume 3).

A equação que fornece o valor do número de Euler é dada a seguir:

$e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$

Nesta equação podemos observar que quanto mais alto o valor de n mais preciso se torna o valor de e.

De maneira simplificada, com base nos conceitos até agora abordados podemos encontrá-la da seguinte maneira:

Se $f(x)=\ln x$ então $f\ '(x)={\frac {1}{x}}$, logo: $f\ '(1)=1$

Por outro lado, pela definição:

$f\ '(x)=\lim _{\alpha \to 0}{\frac {\ln(x+\alpha )-\ln x}{\alpha }}$

Para $f\ '(1)=1$:

$1=\lim _{\alpha \to 0}{\frac {\ln(1+\alpha )-\ln 1}{\alpha }}$

$1=\lim _{\alpha \to 0}{\frac {\ln(1+\alpha )}{\alpha }}$

$1=\lim _{\alpha \to 0}{\frac {1}{\alpha }}\ln(1+\alpha )$

$1=\lim _{\alpha \to 0}\ln(1+\alpha )^{\frac {1}{\alpha }}$

$e=\lim _{\alpha \to 0}(1+\alpha )^{\frac {1}{\alpha }}$

Sendo: $\alpha ={\frac {1}{n}}$ e $\lim _{\alpha \to 0}\alpha =\lim _{n\to \infty }{\frac {1}{n}}$

Concluimos que:

$e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$

Teoremas

A maioria dos teoremas relacionados, têm origem nas conclusões obtidas no estudo do logarítmo natural, dos quais relacionamos os mais usados:

T39 - Soma

Seja a função $f(x,y)=e^{x+y}$, pode-se afirmar que:

$f(x,y)=e^{x}\cdot e^{y}$

Comprovação:

Considerando: $x=\ln \ a$ e $y=\ln \ b$,

$x+y=\ln \ a\ +\ \ln \ b$

$x+y=\ln \ {ab}$

logo:

$e^{x+y}=e^{\ln \ {ab}}$

$e^{x+y}=ab$

sendo: $a=e^{x}$ e $b=e^{y}$,

$e^{x+y}=e^{x}\cdot e^{y}$

O que comprova o teorema.

T40 - Subtração

De forma similar à análise anterior, sendo a função $f(x,y)=e^{x-y}$, pode-se afirmar que:

$f(x,y)={\frac {e^{x}}{e^{y}}}$

Comprovação:

Considerando: $x=\ln \ a$ e $y=\ln \ b$,

$x-y=\ln \ a\ -\ \ln \ b$

$x-y=\ln \ {\frac {a}{b}}$

logo:

$e^{x-y}=e^{\ln {\frac {a}{b}}}$

$e^{x-y}={\frac {a}{b}}$

sendo: $a=e^{x}$ e $b=e^{y}$,

$e^{x-y}={\frac {e^{x}}{e^{y}}}$

O que comprova o teorema.

T41 - Potência

Seja a função $f(x,y)=\left(e^{x}\right)^{y}$, pode-se afirmar que:

$f(x,y)=e^{xy}$

Comprovação:

$f(x,y)=(e^{x})^{y}$

$f(x,y)=e^{{\ln(e^{x})}^{y}}$

$f(x,y)=e^{y\cdot \ln(e^{x})}$

$f(x,y)=e^{y\cdot x}$

O que comprova o teorema.

Derivadas

Consideremos que $f(x)=e^{x}$, e conseqüentemente: $x=\ln f(x)$, se derivarmos implicitamente este expressão:

$dx={\frac {1}{f(x)}}df(x)$

Curiosamente, teremos:

$f(x)={\frac {df(x)}{dx}}$

$f(x)=f\ '(x)$

Ou seja, a função exponencial natural é invariável durante o processo de derivação, o que traz uma série de implicações simplificadoras para estas funções.

Por outro lado se $f(x)=a^{x}$, temos que:

$a=e^{\ln a}$

Fazendo $u=x\cdot \ln a$ e $f(x)=e^{u}$, teremos:

$f\ '(x)=e^{u}\cdot {\frac {du}{{\mbox{d}}x}}$

Se ${\frac {du}{{\mbox{d}}x}}=\ln a$, concluimos que:

$f\ '(x)=a^{x}\cdot \ln a$

Que é adotada como uma derivada mais genérica, pois pode ser empregada em qualquer exponencial, pois inclui correção para o fator da base.

Integrais

Como não poderia ser diferente, o valor da integral da função exponencial natural $f(x)=e^{x}$ é a própria função, conforme a regra da reversibilidade entre a derivada e a integral, apenas sendo necessária a devida observação da base, para eventual correção da diferencial e conseqüente introdução de fator de correção, nos casos em que a função torna-se composta.

Desta forma, temos:

$\int e^{x}dx=e^{x}+C$, 

Sendo C constante.

---

Logarítmicas com outras bases

Como foi visto durante o ensino médio, os logaritmos têm uma definição direta e que denota a sua finalidade de expressar o valor do expoente em uma operação exponencial, a definição pura é dada da seguinte forma:

Se $x=a^{n}$ então,

$\log _{a}x=n$

Onde: a é chamada base do logaritmo, x é o logaritmando e n é o expoente.

O logaritmo é, portanto, a operação pela qual se obtém o expoente necessário para que a base seja elevada, numa operação exponencial e se obtenha o número x.

A função logarítmica de base a pode ser expressa da seguinte forma:

$f(x)=\log _{a}x$

O que nos possibilita encontrar um valor para cada x expresso na equação.

Mudança de base

Analisemos agora a possibilidade de encontrar uma função logarítmica de uma base a e transformá-la em uma função logarítmica de base natural, ou outra base qualquer:

Seja a função $y=\log _{a}x$, podemos dizer que:

$x=e^{\ln x}$ e que $a=e^{\ln a}$,

como: $x=a^{y}$,

$x=(e^{\ln a})^{y}$,

$x=e^{y\cdot \ln a}$,

$\ln x=y\cdot \ln a$,

O que nos possibilita afirmar que:

$y={\frac {\ln x}{\ln a}}$,

ou

$\log _{a}x={\frac {\ln x}{\ln a}}$.

Note que a analogia serve para funções logarítmicas de qualquer base, visto que podemos substituir $\ln x$ por $\log _{z}x$ sendo z a base que substituirá e na análise anterior.

O que nos possibilita considerar que quando temos duas bases, sejam: a e b, podemos promover a troca das bases, de forma que:

$\log _{a}x={\frac {\log _{b}x}{\log _{b}a}}$

Derivadas

A derivada da função logarítmica com base diferente de e pode ser feita por substituição da base. Considerando $f(x)=\log _{a}x$, temos que:

$\log _{a}x={\frac {1}{\ln a}}\cdot \ln x$,

$f(x)={\frac {1}{\ln a}}\cdot \ln x$,

logo:

$f\ '(x)={\frac {d\left({\frac {1}{\ln a}}\cdot \ln x\right)}{dx}}$

$f\ '(x)={\frac {1}{\ln a}}\cdot {\frac {d(\ln x)}{dx}}$

$f\ '(x)={\frac {1}{\ln a}}\cdot {\frac {1}{x}}$

Que nos dá a derivada:

$f\ '(x)={\frac {1}{x\cdot \ln a}}$

---

Trigonométricas I

A trigonometria, tal qual vista na matemática elementar, está relacionada com as relações métricas do triângulo retângulo e do ciclo trigonométrico, agora introduziremos o estudo infinitesimal das funções trigonométricas que são largamente utilizadas nas ciências exatas.

Conceitos básicos (Radianos)

Em um plano definido pelos eixos x e y podemos estabelecer coordenadas cartesianas para cada ponto, o que nos permite identificar cada um dos pontos em qualquer posição do plano, existe outra maneira de encontrar um ponto neste plano; se quisermos estabelecer uma relação triangular podemos determinar a posição de cada ponto no plano da seguinte forma:

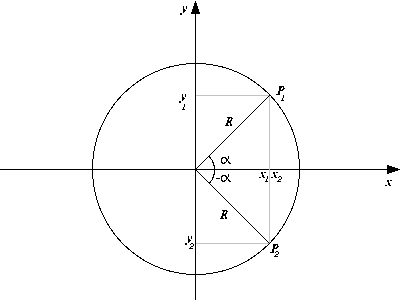
Figura 5

Imagine que cada ponto está numa distãncia R do ponto $(0,0)$ em um plano cartesiano definido por pontos $(x,y)$, da mesma forma a reta R, que é definida entre os pontos $(0,0)\to (x,y)$, forma um ângulo com o eixo x, que chamaremos de $\alpha$, note que podemos identificar qualquer dos pontos no plano a partir de uma reta R e um ângulo $\alpha$.

Observemos que R, quando fixa, é uma reta que determina um conjunto de pontos em torno do ponto $(0,0)$, se fizermos $\alpha$ variar em todos os valores possíveis teremos uma circunferência. Quando fazemos o valor de R variar teremos diferentes valores de x e y, porém a relação entre eles sempre será a mesma.

Curiosamente, há uma relação entre o perímetro do círculo e o seu diâmetro, ela se apresenta constante qualquer que seja o raio do círculo; o resultado desta relação é um número transcedental chamado PI, representado pela letra grega de mesmo nome: $\pi$. Resgatando esta relação para a nossa análise podemos dizer que, se chamarmos o perímetro da circunferência, formada no gráfico, de $l$ e admitirmos um diâmetro de $2R$, então teremos:

${\frac {l}{2R}}=\pi$

Que resulta em:

$l=2\pi R$

Que é uma relação bastante esclarecedora, visto que nos mostra uma dependência linear entre o raio e o comprimento de um fio imaginário que pudesse ser usado para seguir o contorno da circunferência do gráfico. Se o raio for unitário teremos um valor de referência para l, que poderá ser usado para encontrar qualquer comprimento de circunferência no gráfico, bastando para isto multiplicá-lo pelo raio, este valor de referência está ligado à circunferência fechada. Por outro lado, se fizermos com que R se desloque de um ângulo nulo, ou seja, que saia do eixo x em direção a y, formando um ângulo $\alpha$, teremos pedaços de circunferência, que chamamos de arcos, considerando que temos um raio unitário e que percorremos um pedaço da circunferência para cada ângulo "$\alpha$" que tomamos, temos uma correspondência entre ângulo e arco, ou seja: podemos nos referir a arcos como unidades de ângulos, esta unidade angular é chamada de Radiano. Qualquer círculo forma $2\pi$ radianos e todas as relações entre os pontos da circunferência que o contorna e os eixos cartesianos podem ser referenciadas como relações entre partes desta medida.

Como o radiano é uma medida real, isto nos leva a outra questão: O que determina o sinal negativo ou positivo neste valor?

Acontece uma variação destes valores quando nos deslocamos de um ponto a outro da circunferência, quando saimos do eixo x em direção ao ponto $P_{1}$ o ângulo cresce, portanto temos que concluir que é positivo, recuando-o ao encontro do eixo x os valores diminuem, portanto se ultrapassarmos o eixo x o valor deve ser menor que zero, nos revelando um ângulo negativo.

Seno e cosseno

Temos, portanto, uma circunferência dentro do plano cartesiano e seus pontos relacionados ao raio R e ao ângulo $\alpha$, são referenciados pelas variáveis x e y no mesmo plano, agora imaginemos funções para que seja possível a partir do raio e do ângulo encontrar as variáveis, estas funções são o seno e o cosseno.

A função seno, simbolizada como:

$\ {\mbox{sen}}(\alpha )$

Nos dá o valor da variável y, ou seja, a altura do ponto em relação ao zero referencial, no encontro dos eixos, conforme espelhada no eixo y, quando o raio R é unitário, caso não seja fazemos $y=R\ {\mbox{sen}}(\alpha )$.

A função cosseno, simbolizada como:

$\cos(\alpha )$

Nos dá o valor da variável x, ou seja, a distância do ponto em relação ao zero referencial, no encontro dos eixos, conforme espelhada no eixo xquando o raio R é unitário, caso não seja fazemos $x=R\cos(\alpha )$.

As funções seno e cosseno são periódicas, ou seja, pela natureza do ciclo trigonométrico, quando temos um valor em x maior que $2\pi$ temos a representação de um ciclo completo mais um ângulo residual, na verdade o valor representa este ângulo residual, o que nos leva a constatação que sempre será calculado o valor do seno ou cosseno do resto da operação ${\frac {x}{2\pi }}$ quando um ângulo maior que $2\pi$ for sugerido para x.

Observações: Este livro utiliza a notação de funções trigonométricas da lingua portuguesa, também é possível encontrar, em outros livros, as notações $\sin x\ ,\ \cos x$ ou $\sin(x)\ ,\ \cos(x)$ para representação de seno e cosseno respectivamente, utilizadas na língua inglesa.

Alguns valores de senos e cossenos de certos arcos são perfeitamente dedutíveis através da observação do ciclo, são eles:

Senos e cossenos notáveis

Ângulo	0	${\frac {\pi }{2}}$	${\pi }$	${\frac {3\pi }{2}}$
$\ {\mbox{sen}}(x)$	0	1	0	-1
$\cos(x)$	1	0	-1	0

Observando o gráfico podemos também concluir que o sinal do seno é idêntico ao sinal do ângulo, enquanto que o cosseno não acompanha o sinal do ângulo, de forma que cossenos de ângulos negativos são iguais a cossenos dos valores absolutos dos ângulos, ou seja:

sendo $a>0$,

$\ {\mbox{sen}}(-a)=-\ {\mbox{sen}}(a)$

enquanto que:

$\cos(-a)=\cos(a)$

Outros senos e cossenos podem ser obtidos pelas relações métricas no triângulo e são largamente utilizados, são:

Senos e cossenos mais comuns

Ângulo	${\frac {\pi }{6}}$	${\frac {\pi }{4}}$	${\frac {\pi }{3}}$	${\frac {2\pi }{3}}$	${\frac {3\pi }{4}}$	${\frac {5\pi }{6}}$	${\frac {7\pi }{6}}$	${\frac {5\pi }{4}}$	${\frac {4\pi }{3}}$	${\frac {5\pi }{3}}$	${\frac {7\pi }{4}}$	${\frac {11\pi }{6}}$
$\ {\mbox{sen}}(x)$	${\frac {1}{2}}$	${\frac {\sqrt {2}}{2}}$	${\frac {\sqrt {3}}{2}}$	${\frac {\sqrt {3}}{2}}$	${\frac {\sqrt {2}}{2}}$	${\frac {1}{2}}$	$-{\frac {1}{2}}$	$-{\frac {\sqrt {2}}{2}}$	$-{\frac {\sqrt {3}}{2}}$	$-{\frac {\sqrt {3}}{2}}$	$-{\frac {\sqrt {2}}{2}}$	$-{\frac {1}{2}}$
$\cos(x)$	${\frac {\sqrt {3}}{2}}$	${\frac {\sqrt {2}}{2}}$	${\frac {1}{2}}$	$-{\frac {1}{2}}$	$-{\frac {\sqrt {2}}{2}}$	$-{\frac {\sqrt {3}}{2}}$	$-{\frac {\sqrt {3}}{2}}$	$-{\frac {\sqrt {2}}{2}}$	$-{\frac {1}{2}}$	${\frac {1}{2}}$	${\frac {\sqrt {2}}{2}}$	${\frac {\sqrt {3}}{2}}$

Identidades (1)

As equações desta seção são conseqüência das características dos senos e cossenos, seu comportamento cíclico e sua relação com uma circunferência de raio unitário lhes conferem uma excelente operatividade, possibilitando-nos fácil intercâmbio entre as mesmas.

I-1 Identidade relacional básica

As funções seno e cosseno estão relacionadas pela equação:

$sen^{2}(a)+cos^{2}(a)=1$

Comprovação:

Observando o ciclo trigonométrico, temos um triângulo cujos catetos são: $\ {\mbox{sen}}(a)$ e $\cos(a)$ e sua hipotenusa é 1, portanto a identidade é conseqüente do conhecido teorema de Pitágoras.

I-2 Cosseno da soma

Sejam os ângulos a e b, o cosseno de sua soma é:

$\cos(a+b)=\cos(a)\cos(b)-\ {\mbox{sen}}(a)\ {\mbox{sen}}(b)$

Comprovação:

Nos pontos A e B do ciclo trigonométrico, temos os arcos para os ângulos a e b:

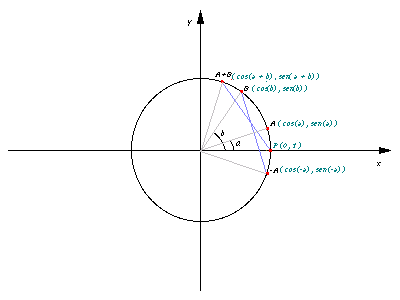
Figura 6

A distância entre os pontos P e (A+B) é igual à distância entre -A e B, o quadrado das duas é:

$[\cos(a+b)-1]^{2}+sen^{2}(a+b)=[\cos(b)-\cos(-a)]^{2}+[\ {\mbox{sen}}(b)-\ {\mbox{sen}}(-a)]^{2}$

Da identidade básica:

$cos^{2}(a+b)-2\cos(a+b)+1+sen^{2}(a+b)=cos^{2}(b)-2\cos(-a)\cos(b)+cos^{2}(-a)+sen^{2}(b)-2\ {\mbox{sen}}(-a)\ {\mbox{sen}}(b)+sen^{2}(-a)$

$cos^{2}(a+b)-2\cos(a+b)+1+1-cos^{2}(a+b)=cos^{2}(b)-2\cos(-a)\cos(b)+cos^{2}(-a)+sen^{2}(b)-2\ {\mbox{sen}}(-a)\ {\mbox{sen}}(b)+sen^{2}(-a)$

$-2\cos(a+b)+1+1=[cos^{2}(b)+sen^{2}(b)]-2\cos(-a)\cos(b)+[cos^{2}(-a)+sen^{2}(-a)]-2\ {\mbox{sen}}(-a)\ {\mbox{sen}}(b)$

$-2\cos(a+b)+2=1-2\cos(-a)\cos(b)+1-2\ {\mbox{sen}}(-a)\ {\mbox{sen}}(b)$

$-2\cos(a+b)=-2\cos(-a)\cos(b)-2\ {\mbox{sen}}(-a)\ {\mbox{sen}}(b)$

$\cos(a+b)=\cos(-a)\cos(b)+\ {\mbox{sen}}(-a)\ {\mbox{sen}}(b)$

Como $\ {\mbox{sen}}(-a)=-\ {\mbox{sen}}(a)$ e $\cos(-a)=\cos(a)$ :

$\cos(a+b)=\cos(a)\cos(b)-\ {\mbox{sen}}(a)\ {\mbox{sen}}(b)$

O que comprova a identidade.

I-3 Cosseno da diferença

Sejam os ângulos a e b, o cosseno de sua diferença é:

$\cos(a-b)=\cos(a)\cos(b)+\ {\mbox{sen}}(a)\ {\mbox{sen}}(b)$

Comprovação:

Do cosseno da soma:

$\cos(a+b)=\cos(a)\cos(b)-\ {\mbox{sen}}(a)\ {\mbox{sen}}(b)$

Substituindo b por -b:

$\cos(a+(-b))=\cos(a)\cos(-b)-\ {\mbox{sen}}(a)\ {\mbox{sen}}(-b)$

$\cos(a-b)=\cos(a)\cos(b)+\ {\mbox{sen}}(a)\ {\mbox{sen}}(b)$

O que comprova a identidade.

I-4 Equivalência angular

Se o ângulo a é ${\frac {\pi }{2}}$ e b é x, então:

$\cos \left({\frac {\pi }{2}}-x\right)=\cos \left({\frac {\pi }{2}}\right)\cos(x)+\ {\mbox{sen}}\left({\frac {\pi }{2}}\right)\ {\mbox{sen}}(x)$

$\cos \left({\frac {\pi }{2}}-x\right)=0+1\cdot \ {\mbox{sen}}(x)$

logo:

$\cos \left({\frac {\pi }{2}}-x\right)=\ {\mbox{sen}}(x)$

Por outro lado, se:

$y=\left({\frac {\pi }{2}}-x\right)$ e

$x=\left({\frac {\pi }{2}}-y\right)$, obtemos:

$\ {\mbox{sen}}\left({\frac {\pi }{2}}-y\right)=\cos(y)$

I-5 Seno da soma

Sejam os ângulos a e b, o seno de sua soma é:

$\ {\mbox{sen}}(a+b)=\ {\mbox{sen}}(a)\cos(b)+\ {\mbox{sen}}(b)\cos(a)$

Comprovação:

Sendo $\cos(a+b)=\cos(a)\cos(b)-\ {\mbox{sen}}(a)\ {\mbox{sen}}(b)$ e $\cos \left[{\frac {\pi }{2}}-(a+b)\right]=\ {\mbox{sen}}(a+b)$, temos:

$\ {\mbox{sen}}(a+b)=\cos \left[{\frac {\pi }{2}}-(a+b)\right]$

$\ {\mbox{sen}}(a+b)=\cos \left[\left({\frac {\pi }{2}}-a\right)-b\right]$

$\ {\mbox{sen}}(a+b)=\cos \left({\frac {\pi }{2}}-a\right)\cos(b)+\ {\mbox{sen}}\left({\frac {\pi }{2}}-a\right)\ {\mbox{sen}}(b)$

$\ {\mbox{sen}}(a+b)=\ {\mbox{sen}}(a)\cos(b)+\ {\mbox{sen}}(b)\cos(a)$

O que comprova a identidade.

I-6 Seno da diferença

Sejam os ângulos a e b, o seno de sua diferença é:

$\ {\mbox{sen}}(a-b)=\ {\mbox{sen}}(a)\cos(b)-\ {\mbox{sen}}(b)\cos(a)$

Comprovação:

Se $\ {\mbox{sen}}(a+b)=\ {\mbox{sen}}(a)\cos(b)+\ {\mbox{sen}}(b)\cos(a)$,

Substituindo b por -b, temos:

$\ {\mbox{sen}}(a-b)=\ {\mbox{sen}}(a)\cos(-b)+\ {\mbox{sen}}(-b)\cos(a)$

e $\ {\mbox{sen}}(-b)=-\ {\mbox{sen}}(b)$ enquanto que $\cos(-b)=\cos(b)$, logo:

$\ {\mbox{sen}}(a-b)=\ {\mbox{sen}}(a)\cos(b)-\ {\mbox{sen}}(b)\cos(a)$

O que comprova a identidade.

I-7 Produto de dois senos

Sejam os ângulos a e b, o produto de seus senos é:

$\ {\mbox{sen}}(a)\ {\mbox{sen}}(b)={\frac {1}{2}}\cdot [\cos(a-b)-\cos(a+b)]$

Comprovação:

Considerando a identidade do cosseno da diferença de dois ângulos e subtraindo de cada um de seus membros os membros correspondentes da identidade do cosseno da soma de dois ângulos:

${\frac {\begin{matrix}\cos(a-b)&=&\ \cos(a)\cos(b)+{\mbox{sen}}(a)\ {\mbox{sen}}(b)\\&-&\\\cos(a+b)&=&\ \cos(a)\cos(b)-{\mbox{sen}}(a)\ {\mbox{sen}}(b)\\\end{matrix}}{\begin{matrix}\cos(a-b)-\cos(a+b)&=&2\ {\mbox{sen}}(a)\ {\mbox{sen}}(b)\end{matrix}}}$

O que comprova a identidade.

I-8 Produto de dois cossenos

Sejam os ângulos a e b, o produto de seus cossenos é:

$\cos(a)\cos(b)={\frac {1}{2}}\cdot [\cos(a+b)+\cos(a-b)]$

Comprovação:

Considerando a identidade do cosseno da soma de dois ângulos e somando a cada um de seus membros os membros correspondentes da identidade do cosseno da diferença de dois ângulos:

${\frac {\begin{matrix}\cos(a+b)&=&\ \cos(a)\cos(b)-{\mbox{sen}}(a)\ {\mbox{sen}}(b)\\&+&\\\cos(a-b)&=&\ \cos(a)\cos(b)+{\mbox{sen}}(a)\ {\mbox{sen}}(b)\\\end{matrix}}{\begin{matrix}\cos(a+b)+\cos(a-b)&=&+2\ {\mbox{cos}}(a)\ {\mbox{cos}}(b)\end{matrix}}}$

O que comprova a identidade.

I-9 Produto de seno e cosseno

Sejam os ângulos a e b, o produto do seno de a pelo cosseno de b é:

$\ {\mbox{sen}}(a)\cos(b)={\frac {1}{2}}\cdot [\ {\mbox{sen}}(a+b)+\ {\mbox{sen}}(a-b)]$

Comprovação:

Considerando a identidade do seno da soma de dois ângulos e somando a cada um de seus membros os membros correspondentes da identidade do seno da diferença de dois ângulos:

${\frac {\begin{matrix}\ {\mbox{sen}}(a+b)&=&\ {\mbox{sen}}(a)\cos(b)+\cos(a)\ {\mbox{sen}}(b)\\&+&\\\ {\mbox{sen}}(a-b)&=&\ {\mbox{sen}}(a)\cos(b)-\cos(a)\ {\mbox{sen}}(b)\\\end{matrix}}{\begin{matrix}\ {\mbox{sen}}(a+b)+\ {\mbox{sen}}(a-b)&=&2\ {\mbox{sen}}(a)\cos(b)\end{matrix}}}$

O que comprova a identidade.

I-10 Soma de dois senos

Sejam os ângulos p e q, a soma dos senos de p e de q é:

$\ {\mbox{sen}}(p)+\ {\mbox{sen}}(q)=2\ {\mbox{sen}}\left({\frac {p+q}{2}}\right)\cos \left({\frac {p-q}{2}}\right)$

Comprovação:

Podemos dizer que:

${\frac {\left\{{\begin{matrix}a+b&=&p\\&+&\\a-b&=&q\end{matrix}}\right.}{\begin{matrix}&&&2a&=&p+q\\\\a&=&{\frac {p+q}{2}}&;&b&=&{\frac {p-q}{2}}\end{matrix}}}$

substituindo na identidade:

${\begin{matrix}\ {\mbox{sen}}(a+b)+\ {\mbox{sen}}(a-b)&=&2\ {\mbox{sen}}(a)\cos(b)\\\ {\mbox{sen}}(p)+\ {\mbox{sen}}(q)&=&2\ {\mbox{sen}}\left({\frac {p+q}{2}}\right)\cos \left({\frac {p-q}{2}}\right)\end{matrix}}$

O que comprova a identidade.

I-11 Soma de dois cossenos

Sejam os ângulos p e q, a soma dos cossenos de p e de q é:

$\cos(p)+\cos(q)=2\cos \left({\frac {p+q}{2}}\right)\cos \left({\frac {p-q}{2}}\right)$

Comprovação:

Seguindo a analogia anterior:

${\begin{matrix}\cos(a+b)+\cos(a-b)&=&2\cos(a)\cos(b)\\\cos(p)+\cos(q)&=&2\cos \left({\frac {p+q}{2}}\right)\cos \left({\frac {p-q}{2}}\right)\end{matrix}}$

O que comprova a identidade.

I-12 Diferença de dois senos

Sejam os ângulos p e q, a diferença dos senos de p e de q é:

$\ {\mbox{sen}}(p)-\ {\mbox{sen}}(q)=2\cos \left({\frac {p+q}{2}}\right)\ {\mbox{sen}}\left({\frac {p-q}{2}}\right)$

Comprovação:

substituindo q por -q em:

${\begin{matrix}\ {\mbox{sen}}(p)+\ {\mbox{sen}}(q)&=&2\ {\mbox{sen}}\left({\frac {p+q}{2}}\right)\cos \left({\frac {p-q}{2}}\right)\\\ {\mbox{sen}}(p)+\ {\mbox{sen}}(-q)&=&2\ {\mbox{sen}}\left({\frac {p-q}{2}}\right)\cos \left({\frac {p+q}{2}}\right)\end{matrix}}$

O que comprova a identidade.

I-13 Diferença de dois cossenos

Sejam os ângulos p e q, a diferença dos cossenos de p e de q é:

$\cos(p)-\cos(q)=-2\cos \left({\frac {p+q}{2}}\right)\cos \left({\frac {p-q}{2}}\right)$

Comprovação:

substituimos q e q, por ${\frac {p+q}{2}}$ e ${\frac {p-q}{2}}$ em:

${\begin{matrix}\cos(a-b)-\cos(a+b)&=&2\cos(a)\cos(b)\\\cos(q)-\cos(p)&=&2\cos \left({\frac {p+q}{2}}\right)\cos \left({\frac {p-q}{2}}\right)\\\cos(p)-\cos(q)&=&-2\cos \left({\frac {p+q}{2}}\right)\cos \left({\frac {p-q}{2}}\right)\end{matrix}}$

O que comprova a identidade.

Limíte trigonométrico fundamental

Precisaremos de um limite fundamental nas próximas seções, se trata de um limite que é utilizado na dedução das derivadas do seno e do cosseno, faremos sua dedução nesta seção. Considere o ciclo trigonométrico representado a seguir:

Figura 7

A figura 7 mostra a representação de um ângulo $\alpha$ no ciclo trigonométrico, o nosso propósito é deduzir o seguinte limite:

$\lim _{\alpha \to 0}{\frac {\ {\mbox{sen}}(\alpha )}{\alpha }}$

Para isto, imagine o triângulo inscrito na circunferência, podemos dizer que o segmento de reta n é uma aproximação grosseira do arco $\alpha$, porém observe que quando o ângulo se aproxima de zero o segmento se torna mais parecido com o respectivo ângulo, algébricamente podemos expressar que:

$\lim _{\alpha \to 0}{\frac {1}{\alpha }}=\lim _{n\to 0}{\frac {1}{n}}$

Por outro lado façamos o cálculo do valor do n; observando o triângulo podemos dizer que:

$n^{2}=sen^{2}(\alpha )+[1-\cos(\alpha )]^{2}$

$n^{2}=2[1-\cos(\alpha )]$

Logo:

$cos(\alpha )=\left(1-{\frac {n^{2}}{2}}\right)$

$1-sen^{2}(\alpha )=\left(1-{\frac {n^{2}}{2}}\right)^{2}$

Simplificando temos:

$\ {\mbox{sen}}(\alpha )=n\left[1-{\frac {n^{2}}{4}}\right]^{\frac {1}{2}}$

Voltando para o nosso limite, temos que usar as nossas equações anteriores desta forma:

$\left[\lim _{\alpha \to 0}{\frac {1}{\alpha }}=\lim _{n\to 0}{\frac {1}{n}}\right]\cdot \ {\mbox{sen}}(\alpha )$

$\lim _{\alpha \to 0}{\frac {\ {\mbox{sen}}(\alpha )}{\alpha }}=\lim _{n\to 0}{\frac {\ {\mbox{sen}}(\alpha )}{n}}$

Substituindo o valor do seno no lado da equação relaciondado ao n, teremos:

$\lim _{\alpha \to 0}{\frac {\ {\mbox{sen}}(\alpha )}{\alpha }}=\lim _{n\to 0}\left[1-{\frac {n^{2}}{4}}\right]^{\frac {1}{2}}$

O que nos leva ao resultado:

$\lim _{\alpha \to 0}{\frac {\ {\mbox{sen}}(\alpha )}{\alpha }}=1$

A interpretação desse limite é a seguinte:

Uma vez que o ângulo diminui até valores próximos de zero e o arco tende a se assemelhar a uma reta em regiões próximas do zero, o valor do seno é igual ao valor do arco no limite, quando o seu valor se aproxima de ser nulo.

Derivada do seno

Agora podemos verificar qual a variação da função seno em relação ao seu ângulo, aplicando a definição da derivada ao seno, temos:

$f(x)=\ {\mbox{sen}}(x)$

$f\ '(x)=\lim _{h\to 0}{\frac {\ {\mbox{sen}}(x+h)-\ {\mbox{sen}}(x)}{h}}$

Aplicando o seno da soma:

$f\ '(x)=\lim _{h\to 0}{\frac {\ {\mbox{sen}}(x)\cos(h)+\ {\mbox{sen}}(h)\cos(x)-\ {\mbox{sen}}(x)}{h}}$

$f\ '(x)=\lim _{h\to 0}{\frac {\ {\mbox{sen}}(x)\cos(h)}{h}}+\lim _{h\to 0}{\frac {\ {\mbox{sen}}(h)\cos(x)}{h}}-\lim _{h\to 0}{\frac {\ {\mbox{sen}}(x)}{h}}$

Aplicando os limites:

$f\ '(x)=\lim _{h\to 0}{\frac {\ {\mbox{sen}}(h)}{h}}\cos(x)$

Temos, então, o limite fundamental que é igual a 1, logo:

$f\ '(x)=\cos(x)$

Derivada do cosseno

Também podemos verificar qual a variação da função cosseno em relação ao seu ângulo, aplicando a definição da derivada ao cosseno, temos:

$f(x)=\cos(x)$

$f\ '(x)=\lim _{h\to 0}{\frac {\cos(x+h)-\cos(x)}{h}}$

Aplicando o seno da soma:

$f\ '(x)=\lim _{h\to 0}{\frac {\cos(x)\cos(h)-\ {\mbox{sen}}(x)\ {\mbox{sen}}(h)-\cos(x)}{h}}$

$f\ '(x)=\lim _{h\to 0}{\frac {\cos(x)\cos(h)}{h}}-\lim _{h\to 0}{\frac {\ {\mbox{sen}}(x)\ {\mbox{sen}}(h)}{h}}-\lim _{h\to 0}{\frac {\cos(x)}{h}}$

Aplicando os limites:

$f\ '(x)=\lim _{h\to 0}-{\frac {\ {\mbox{sen}}(h)}{h}}\ {\mbox{sen}}(x)$

Novamente temos o limite fundamental, logo:

$f\ '(x)=-\ {\mbox{sen}}(x)$

Integral do seno

Como conseqüência do resultado da derivada do seno, podemos deduzir que a sua integral, como operação inversa é:

$\int \ {\mbox{sen}}(x)dx=-\cos(x)+C$

Cuja constante C é a constante devido a indefinição no processo de antidiferenciação, conforme já estudamos anteriormente.

Integral do cosseno

Segundo o mesmo princípio colocado no caso da integral do seno, podemos afirmar que a operação de integração do cosseno é definida por:

$\int \cos(x)dx=\ {\mbox{sen}}(x)+C$

Cuja constante C é a constante devido a indefinição no processo de antidiferenciação