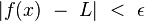Discussão:Cálculo (Volume 1)/Limites e Continuidade
Sobre este espaço de discussão
Infinito
Googolplex
- Que tal fazer uma pequena referencia ao Googolplex nesta seção? Pode ser interessante...
Nesta seção está escrito:
"Pois bem este não é infinito, pois aqui, falaremos desse número como sendo algo tão..."
Acredito que não devemos tratar o infinito como número, pelo menos não neste contexto.
Aqui o que conta é a o comportamento de  , quando
, quando  é suficientemente grande;
mas não o valor de
é suficientemente grande;
mas não o valor de  quado x é um número infinito. Pelo menos no cálculo, não lidamos com cardinais transfinitos, então não é bom que os leitores pensem que x é igual a um tipo de infinito...
Podemos, no entanto, criar links para os tópicos correspondentes da wikipedia, para que eles procurem identificar a diferença....
quado x é um número infinito. Pelo menos no cálculo, não lidamos com cardinais transfinitos, então não é bom que os leitores pensem que x é igual a um tipo de infinito...
Podemos, no entanto, criar links para os tópicos correspondentes da wikipedia, para que eles procurem identificar a diferença....
- Fazer referências e adições de texto, que enriqueçam o conteúdo é algo perfeitamente plausível, porém a maneira de lidar com a explanação inicial, que está destacada no início do comentário é subjetiva, este livro é didático e a sua idéia inicial é fazer a transição do pensamento de nível médio para nível universitário gradativamente, acho que a frase pode ficar como está e um parágrafo a seguir faça a explanação mais aprofundada. Algo do tipo: Apesar de não termos como classificar infinito como exatamente um número... --Marcos A. N. de Moura 14h47min de 29 de Setembro de 2007 (UTC)
Números grandes, tendências, infinito...
- É bem diferente falar de um número muito grande (um número real, por exemplo o Googol) e falar de um número transfinito... Nesse sentido, acho que poderíamos mudar frases como:
"Infinito é uma tendência..." e o que é uma tendência?
- Mudar? Qual é exatamente a idéia mais apropriada neste caso? --Marcos A. N. de Moura 14h47min de 29 de Setembro de 2007 (UTC)
- Fiz uma nova leitura. Acho que tinha entendido tendência de outro jeito, mas agora sei o que quiz dizer (espero!). Fiz algumas pequenas correções no texto. Veja se aprova...
-
 Feito Helder 23h50min de 5 de Outubro de 2007 (UTC)
Feito Helder 23h50min de 5 de Outubro de 2007 (UTC)
- "Desta forma é um número que só podemos representar como um limite..." tem outros jeitos sim!
e outras do gênero, levando em conta que certos infinitos tem uma formulação matemática precisa.... Helder 20h34min de 28 de Setembro de 2007 (UTC)
- Enfim, isto é uma questão de escopo, lembre-se e terá que aprender a lidar com isto aqui, que isto não é uma enciclopédia, cada livro tem que se adequar ao escopo de estudo e no máximo reportar referências para maiores detalhes. Para isto, já que não concorda com: "só podemos representar como" o mais coerente para este livro e capítulo seria algo como: " só podemos, por enquanto, representar como". --Marcos A. N. de Moura 14h47min de 29 de Setembro de 2007 (UTC)
- Ok! Vou me manter no escopo ao qual o livro é proposto. Do que eu disse sobre a frase "é um número que só podemos representar como um limite", penso o seguinte: ao definir limites "no infinito", me parece que se pretende normalmente é analisar o comportamento da função quando os valores são muito grandes (ou muito pequenos), e não representar o infinito. Entende? Por isso acho que devemos mudar o foco da seção. Por exemplo:
- Concordo em começar a seção apresentando algumas idéias do que seja o infinito (continuar falando em números muito grandes, valores inatingiveis, caminhos sem fim...). Isso ajuda a intuir as definições que vem depois.

- ==>OK! --Marcos A. N. de Moura 18h35min de 30 de Setembro de 2007 (UTC)
 Feito Helder 23h50min de 5 de Outubro de 2007 (UTC)
Feito Helder 23h50min de 5 de Outubro de 2007 (UTC)
- ==>Neste nível, sem propor uma abstração maior, a idéia é imaginar infinito como um número que não é possível de se alcançar. Acredito que para uma análise inicial esta visão serve muito bem. Porém, se deseja mudar a linha de pensamento fique a vontade, mas a necessidade de um horizonte onde se deva estabelecer a visão do foco ainda se mantém, nem todas as pessoas podem aprender sem visualizar um objeto final. --Marcos A. N. de Moura 18h35min de 30 de Setembro de 2007 (UTC)
-
 Feito Alterei o enfoque, sem perder de vista o carater introdutório da seção. Helder 23h50min de 5 de Outubro de 2007 (UTC)
Feito Alterei o enfoque, sem perder de vista o carater introdutório da seção. Helder 23h50min de 5 de Outubro de 2007 (UTC) -
 Desfeito. Vamos retomar.
Desfeito. Vamos retomar.
- Concordo em começar a seção apresentando algumas idéias do que seja o infinito (continuar falando em números muito grandes, valores inatingiveis, caminhos sem fim...). Isso ajuda a intuir as definições que vem depois.
- Ok! Vou me manter no escopo ao qual o livro é proposto. Do que eu disse sobre a frase "é um número que só podemos representar como um limite", penso o seguinte: ao definir limites "no infinito", me parece que se pretende normalmente é analisar o comportamento da função quando os valores são muito grandes (ou muito pequenos), e não representar o infinito. Entende? Por isso acho que devemos mudar o foco da seção. Por exemplo:
No momento, está escrito:
Desta forma é um "número"(1), apenas como suposição inicial. Este é na realidade um ente matemático que nunca poderemos alcançar(3), que só podemos representar(2) como um limite neste momento... Então façamos um estudo de como representá-lo(2). No início deste capítulo, discutimos como analisar o comportamento de uma função (sua tendência) quando a variável se aproxima de um número em seu domínio. Nesta seção, discutiremos duas situações novas:
- O que acontece com os valores de
 , quando
, quando  é muito grande?
é muito grande? - O que fazer quando, ao aproximar
 de um ponto
de um ponto  , os valores de
, os valores de  ficam cada vez maiores?
ficam cada vez maiores?
Usaremos o termo "infinito" sempre que for preciso lidar com "números gigantescos", no sentido de serem "tão grandes que nunca poderemos alcançar". Deste modo, também poderemos representar as duas situações acima usando conceitos de limite. Façamos então um estudo destes novos tipos de limite.
- Ao supor que o infinito é um número, estamos admitindo que ele tem as mesmas propriedades que os demais números (no caso do cálculo, os reais). O que não é verdade.
- Sugestão: Desta forma é como se fosse um "número". E não precisamos falar de suposição inicial, já que ainda estamos lidando com idéias intuitivas neste parágrafo.
- Uma vez que o primeiro parágrafo sugere ao leitor o que ele pode entender pelo termo "infinito", acho importante deixar claro que este termo será usado para falar sobre a função. São as propriedades dela (suas tendências, seu crescimento, etc) que serão estudadas depois deste parágrafo introdutório. Por isso, não me parece adequado dar a entender que a seguir estudaremos como representá-lo (o infinito). O que queremos estudar é a função. As propriedades dela serão representadas por termos como "infinito" e "tendências infinitas", que já foram apresentados de forma intuitiva. Daí em diante, faz-se a ligação do conceito apresentado informalmente, com as propriedades das funções reais.
- Sugestão: Focar o texto nas propriedades relacionadas ao infinito (já conceituado) e não no infinito.
- Não acho prudente dizer que o infinito é na verdade "tal coisa", se "tal coisa" não disser o que ele realmente é. E no cálculo ele é só uma notação, um termo usado ao dar significado às características das funções. Em outros contextos é número (ex: aritimética transfinita).
- Sugestão: Se vamos dizer coisas informais como "um ente matemático que nunca poderemos alcançar", recomendo não dizer "na realidade", pois a realidade é outra (tanto no cálculo quanto em outros contextos).Helder 01h24min de 9 de Outubro de 2007 (UTC)
- OK! Marcos A. N. de Moura 15h56min de 9 de Outubro de 2007 (UTC)
- Para isto tenho uma sugestão sintetizada:
- Desta forma é como se fosse um "número", apenas como suposição inicial. Este é um ente matemático que nunca poderemos alcançar, que só podemos imaginar o que aconteceria caso um limite suficientemente alto fosse estabelecido... Então façamos um estudo de como podemos avaliar comportamentos de funções supondo valores extremamente altos em relação as expressões como um todo.
- Melhor? --Marcos A. N. de Moura 15h56min de 9 de Outubro de 2007 (UTC)
- Sim. Mas algumas coisas parecem meio incompletas:
- Desta forma é como se fosse um "número", apenas como suposição inicial. Este é um ente matemático que nunca poderemos alcançar, que só podemos imaginar o que aconteceria (com quem?) caso um limite (o termo é "limite" mesmo?) suficientemente alto fosse estabelecido (como se estabelece isso? não entendi o procedimento)... Então façamos um estudo de como podemos avaliar comportamentos de funções supondo valores extremamente altos (valores de quem? x, f(x) ou o que?) em relação as expressões como um todo (qual expressão, a da f(x)? ou outra?).
- Poderia explicar (pra mim) o que quiz dizer? Aí digo se concordo... ou se acrescentamos também o que vc me explicar...
- Vamos lá:
- Desta forma é como se fosse um "número", apenas como suposição inicial. Este é um ente matemático que nunca poderemos alcançar, caso este ente estiver incluso em uma equação, só podemos imaginar o que aconteceria com a mesma caso um valor suficientemente alto, em relação ao outros membros desta, fosse estabelecido. Então façamos um estudo de como podemos avaliar comportamentos de funções supondo valores extremamente altos para a variável que tende a infinito, em relação à equação como um todo.
- Acha que fica melhor assim?
- Obviamente, deve imaginar a qual procedimento me refiro... Quando levamos a variável sob o limite a valores suficientemente altos em relação a todos os membros da equação temos como avaliar qual o valor do limite, pois via de regra, o método utilizado para resolução que desejo expor é o que elimina termos com denominadores que tendem a infitito, cujo valor é nulo. --Marcos A. N. de Moura 16h05min de 10 de Outubro de 2007 (UTC)
- Finalmente entendi do que estava sendo falado, e a qual procedimento se referia. Isso mudou a forma como eu via o parágrafo em relação aos que estão em volta. Proponho então mover o texto e colocar depois de "Deste modo, também poderemos representar as duas situações acima usando conceitos de limite.
Façamos então um estudo destes novos tipos de limite.", com a seguinte "cara":
- Finalmente entendi do que estava sendo falado, e a qual procedimento se referia. Isso mudou a forma como eu via o parágrafo em relação aos que estão em volta. Proponho então mover o texto e colocar depois de "Deste modo, também poderemos representar as duas situações acima usando conceitos de limite.
- Para isso, quando realizarmos um cálculo, podemos tratar o infinito como se fosse um "número", embora este seja um ente matemático que nunca poderemos alcançar. Caso a variável
 esteja tendendo ao infinito, e apareça em uma expressão, podemos imaginar o que aconteceria com a expressão caso
esteja tendendo ao infinito, e apareça em uma expressão, podemos imaginar o que aconteceria com a expressão caso  fosse um número suficientemente grande. Então façamos um estudo de como podemos avaliar o comportamento das funções quando a variável tende a infinito.
fosse um número suficientemente grande. Então façamos um estudo de como podemos avaliar o comportamento das funções quando a variável tende a infinito. - Acho que ficará melhor nesse lugar, depois de termos dito que há duas situações novas, começamos a falar dessa em particular... O que acha? Helder 18h42min de 10 de Outubro de 2007 (UTC)
- Exatamente!!!
 Podemos colocar este parágrafo!!!--Marcos A. N. de Moura 01h12min de 11 de Outubro de 2007 (UTC)
Podemos colocar este parágrafo!!!--Marcos A. N. de Moura 01h12min de 11 de Outubro de 2007 (UTC)
 Feito Coloquei o parágrafo no lugar proposto e acertei alguns detalhes no texto (também troquei o "falaremos desse número como sendo" por "falaremos do infinito como sendo" no primeiro parágrafo, para ficar com o mesmo sentido de "como se fosse um número" OK?). Helder 13h52min de 11 de Outubro de 2007 (UTC)
Feito Coloquei o parágrafo no lugar proposto e acertei alguns detalhes no texto (também troquei o "falaremos desse número como sendo" por "falaremos do infinito como sendo" no primeiro parágrafo, para ficar com o mesmo sentido de "como se fosse um número" OK?). Helder 13h52min de 11 de Outubro de 2007 (UTC)
- Exatamente!!!
- Outra coisa, a frase "Este é um ente matemático que nunca poderemos alcançar" (neste parágrafo) me parece apenas uma repetição do que foi dito no parágrafo anterior no texto "uma forma de representar algo que é tão alto que jamais poderíamos atingir". Independente disso, acho que ficaria bom deixar os dois parágrafos em um só. E neste caso, prefiro deixar o "uma forma de representar algo que é tão alto que jamais poderíamos atingir", e não duplicar a mesma informação. Helder 12h43min de 10 de Outubro de 2007 (UTC)
- OK! Podemos sintetizar... --Marcos A. N. de Moura 16h05min de 10 de Outubro de 2007 (UTC)
 Feito Aproveitei a inclusão anterior (do parágrafo logo acima) para fazer a síntese, removendo uma das ocorrencias e mantendo a que aparece no parágrafo acertado. Helder 13h55min de 11 de Outubro de 2007 (UTC)
Feito Aproveitei a inclusão anterior (do parágrafo logo acima) para fazer a síntese, removendo uma das ocorrencias e mantendo a que aparece no parágrafo acertado. Helder 13h55min de 11 de Outubro de 2007 (UTC)
- OK! Podemos sintetizar... --Marcos A. N. de Moura 16h05min de 10 de Outubro de 2007 (UTC)
- Mais Adiante, temos:
- Antes de mais nada pensemos qual a melhor maneira de aumentar sucessivamente o valor de uma função(1) neste caso, isto é possível fazendo divisões por números menores que 1(2). Obviamente existem inúmeras formas de criar uma função que aumenta seu valor sucessivamente, usaremos esta pois nos ajuda a eliminar números racionais que nos trazem mais dificuldades de operação, como veremos logo adiante.
- Vejamos um exemplo de uma função que aumenta sucessivamente os seus valores, quando a variável se aproxima de um determinado ponto. Uma possibilidade é usar divisões por números positivos muito pequenos (próximos de zero).
- Primeiramente, note que eu adicionei o parágrafo procurando substituir o primeiro, mantendo as idéias tratadas. Os motivos são os seguintes:
- Ao falar de como fazer tal coisa com o valor de uma função, dá-se a impressão de que foi dada uma função (pelos autores), e que os leitores têm a tarefa de descobrir como fazer a tal coisa com a função fixada. As alterações tinham a intensão de tornar mais claro o que se queria. Me parece que a proposta era induzir o leitor a criar uma função com determinada característica.
- Sugestão: Me pareceu que "uma função que aumenta sucessivamente os seus valores, quando a variável se aproxima de um determinado ponto" traduzia melhor sua intensão (que foi melhor apresentada quando você disse "existem inúmeras formas de criar uma função que aumenta seu valor sucessivamente"). Estou certo?
- A troca de "menores que 1" por "positivos muito pequenos (próximos de zero)", foi só pra enfatizar que a variável está se aproximando do zero, e não apenas ficando menor que 1.
- Sugestão: Podemos deixar o 1, se preferir assim.
- Quanto a justificar a escolha de uma certa função (pelos autores) como se fosse para "nos ajuda a eliminar números racionais que nos trazem mais dificuldades de operação", acho que isso não está correto. Primeiro porque isso não elimina os números racionais. Segundo, porque não percebo em que sentido os números racionais trazem dificuldades de operação. Tem coisa mais simples do que uma fração???

- O que quiz dizer?
- OBS: Note que mais adiante foi justificada a escolha de determinada função:
- Poderíamos então usar a função
 , embora, naturalmente, existam inúmeras funções que aumentam seus valor conforme
, embora, naturalmente, existam inúmeras funções que aumentam seus valor conforme  tende a zero. Não usaremos
tende a zero. Não usaremos 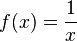 , pois assim evitamos um comportamento diferente para números negativos próximos de zero.
, pois assim evitamos um comportamento diferente para números negativos próximos de zero.
- Poderíamos então usar a função
- Precisamos repetir lá em cima? Helder 01h57min de 9 de Outubro de 2007 (UTC)
- Bem, vejo que estes parágrafos não estão claros a respeito do propósito da escolha da função com denominador variável... Na verdade a intenção aqui é a de dar uma visão inicial para os casos das eliminações de termos com denominadores que tendem ao infinito, ou seja, funções que têm termos tais quais:

- O que nos permite fazer:
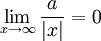
- Por isso sugiro adaptar os parágrafos para:
- Considerando uma função racional, tal que:
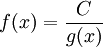
- Pensemos na melhor maneira de aumentar sucessivamente o valor desta função. isto é possível fazendo com que
 forneça valores menores que 1. Obviamente existem inúmeras formas de criar funções que aumentam seu valor sucessivamente, usaremos esta pois nos ajuda a eliminar números racionais que nos trazem mais dificuldades na análise dos resultados, como veremos logo adiante.
forneça valores menores que 1. Obviamente existem inúmeras formas de criar funções que aumentam seu valor sucessivamente, usaremos esta pois nos ajuda a eliminar números racionais que nos trazem mais dificuldades na análise dos resultados, como veremos logo adiante. - O mais importante aqui é notar que quanto mais
 aumenta, mais próximo de zero aproxima-se a função
aumenta, mais próximo de zero aproxima-se a função 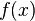 .
.
- Já está bem mais claro. Gostei de usar funções racionais, e acho que seria bom acrescentar que g(x) é um polinômio (isso pode ser enfatizado por escrito, e também usando p(x) e mvez de g(x)). O que acha? Fora isso, temos que corrigir alguns pontos:
- Fazer "com que
 forneça valores menores que 1" não garante que faremos a função racional f(x) aumentar seus valores. Por exemplo, se a função g(x) for de um tipo que assume valores menores do que 1, e que cresce conforme variamos x, então a função f(x) vai estar diminuido, e não é o que queremos no exemplo...
forneça valores menores que 1" não garante que faremos a função racional f(x) aumentar seus valores. Por exemplo, se a função g(x) for de um tipo que assume valores menores do que 1, e que cresce conforme variamos x, então a função f(x) vai estar diminuido, e não é o que queremos no exemplo...
- Por isso, eu proponho trocar "Antes de mais nada pensemos qual a melhor maneira de aumentar sucessivamente o valor de uma função neste caso, isto é possível fazendo divisões por números menores que 1" por "Antes de mais nada, pensemos qual a melhor maneira de construir uma função que aumenta sucessivamente os seus valores, quando a variável se aproxima de um determinado ponto. Uma possibilidade é usar divisões por números positivos muito pequenos, que se aproximam de zero".
- Quando você sugere eliminar problemas com "números racionais", para facilitar a análise, você se refere a "frações" ou "decimais"? Em que sentido eles atrapalham a análise?
- A resposta dessa pergunta poderia muito bem figurar entre parentesis logo após a frase que comenta sobre isso no texto. Que tal? Helder 12h43min de 10 de Outubro de 2007 (UTC)
- Ah, desculpe a falta de rigor, preciso corrigir isto em mim...
- Na verdade esqueci de mencionar que
 é decrescente para a parte do parágrafo, desta forma:
é decrescente para a parte do parágrafo, desta forma:
- Pensemos na melhor maneira de aumentar sucessivamente o valor desta função. isto é possível fazendo com que
 forneça valores cada vez menores que 1. Obviamente existem inúmeras formas de criar funções que aumentam seu valor sucessivamente, usaremos esta pois nos ajuda a entender um processo de eliminação números racionais que nos trazem mais dificuldades na análise dos resultados, como veremos logo adiante.
forneça valores cada vez menores que 1. Obviamente existem inúmeras formas de criar funções que aumentam seu valor sucessivamente, usaremos esta pois nos ajuda a entender um processo de eliminação números racionais que nos trazem mais dificuldades na análise dos resultados, como veremos logo adiante. - O mais importante aqui é notar que quando fazemos o inverso, ou seja, quando fazemos
 aumentar, a função
aumentar, a função 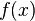 aproximar-se de zero .
aproximar-se de zero . - Acho que desta vez ficou mais claro, acha que está bom? --Marcos A. N. de Moura 01h12min de 11 de Outubro de 2007 (UTC)
- Pensemos na melhor maneira de aumentar sucessivamente o valor desta função. isto é possível fazendo com que
- Não podemos dizer que a mesma é polinomial, poderia ser qualquer função decrescente;
- De fato. Qualquer função decrescente serviria, desde que decrescesse para zero (senão não serve. O que serve são as funções g, positivas, que vão pra zero, sendo ou não decrescentes. Não haveria problema algum se g oscilasse...).
- Sobre usar um polinômio, sugeri isso porque você escreveu "função racional", termo que costuma ser reservado para quocientes entre funções polinomiais. Helder 14h50min de 11 de Outubro de 2007 (UTC)
- A dificuldade de análise a que me refiro está no processo algébrico mesmo... Ou seja, se não tivéssemos como eliminar os termos com denominadores, algumas expressões ficariam enormes.
- Compreendo. Podemos então não "culpar" os números racionais pelas dificuldades de análise, mas sim as "expressões envolvendo quocientes complicados", ou algo assim? "Número racional" lembra frações numéricas, que são de fácil entendimento...
- Resumindo, acho que podemos também poupar os leitores das nossas divagações sobre a g(x), e usar o exemplo simples mesmo. Proponho então:
- Na verdade esqueci de mencionar que
- Considerando uma função definida como:
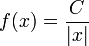
- Pensemos na melhor maneira de variar x para aumentar sucessivamente o valor desta função. Isto é possível fazendo com que
 forneça valores que diminuem até zero. É importante notar que quanto mais
forneça valores que diminuem até zero. É importante notar que quanto mais  diminui, mais os valores da função
diminui, mais os valores da função 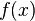 aumentam.
aumentam. - Obviamente existem inúmeras formas de criar funções que aumentam seu valor sucessivamente. Usaremos esta pois nos ajuda a evitar expressões como quociente de funções complicadas ou composição de várias funções. Assim eliminamos dificuldades desnecessárias na análise dos resultados que veremos logo adiante.Helder 14h50min de 11 de Outubro de 2007 (UTC)
- Ótimo, acho que podemos incluí-lo desta maneira.
 --Marcos A. N. de Moura 01h09min de 12 de Outubro de 2007 (UTC)
--Marcos A. N. de Moura 01h09min de 12 de Outubro de 2007 (UTC)
- Ótimo, acho que podemos incluí-lo desta maneira.
- Não acho que deveríamos dizer que faremos um estudo de "como representá-lo", mas sim um estudo "da função" (afinal o cálculo é feito principalmente para se estudar funções). A função será estudada: (1) quando os valores de x "são muito grandes", ou seja, "tendem ao infinito" (
 ) e (2) quando a função "cresce muito", "tendendo ao infinito" se aproximamos x de um certo ponto (
) e (2) quando a função "cresce muito", "tendendo ao infinito" se aproximamos x de um certo ponto (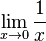 )
)
- ==>Ok, mudemos para: Estudo de como podemos aproximar o valor de funções que se aproximam dele --Marcos A. N. de Moura 18h35min de 30 de Setembro de 2007 (UTC)
-
 Feito Alterei o enfoque, procurando enfatizar o interesse em analisar a função em vez do infinito.Helder 23h50min de 5 de Outubro de 2007 (UTC)
Feito Alterei o enfoque, procurando enfatizar o interesse em analisar a função em vez do infinito.Helder 23h50min de 5 de Outubro de 2007 (UTC)
- Mudar o título "Tendências infinitas" para "limites no Infinito" ou "tendencias no infinito"... (pensando bem, acho que isso é só uma questão de gosto...)
- ==>Desta vez o seu gosto, pode lhe trazer contradição, pois a semântica da expressão "no infitito" traz a idéia de objeto para infinito... O que você contesta.
 --Marcos A. N. de Moura 18h35min de 30 de Setembro de 2007 (UTC)
--Marcos A. N. de Moura 18h35min de 30 de Setembro de 2007 (UTC)
-
 Feito Como era essencialmente questão de gosto, preferi não alterar. podemos usar as duas expressões como sinonimos, indiferentemente.Helder 23h50min de 5 de Outubro de 2007 (UTC)
Feito Como era essencialmente questão de gosto, preferi não alterar. podemos usar as duas expressões como sinonimos, indiferentemente.Helder 23h50min de 5 de Outubro de 2007 (UTC)
- ==>Desta vez o seu gosto, pode lhe trazer contradição, pois a semântica da expressão "no infitito" traz a idéia de objeto para infinito... O que você contesta.
- Sobre "a melhor maneira de aumentar sucessivamente o valor de uma função". Acho que a melhor é "somar 1". Brincadeira...
 (mas é que eu não teria pensado em ficar dividindo por um numero menor que 1..)
(mas é que eu não teria pensado em ficar dividindo por um numero menor que 1..)
- ==>A melhor maneira, para a presente análise. Pode-se fazer uma introdução sobre as implicações de números racionais para a análise. --Marcos A. N. de Moura 18h35min de 30 de Setembro de 2007 (UTC)
-
 Feito Precisei alterar a função para 1/|x|, pois a outra tendia a menos infinito quando x ia pra zero pela esquerda. acho que não trará + problemasHelder 23h50min de 5 de Outubro de 2007 (UTC)
Feito Precisei alterar a função para 1/|x|, pois a outra tendia a menos infinito quando x ia pra zero pela esquerda. acho que não trará + problemasHelder 23h50min de 5 de Outubro de 2007 (UTC)
- "infinito matemático"? o que é isso? Eu acho que o correto é só "infinito"...
- ==>Bem, seríamos um tanto soberbos em despresar: O infinito filosófico, o infinito poético, o infinito religioso... (Lendo, o início do pensamento sobre infinito você verá o porquê desta expressão)
 --Marcos A. N. de Moura 18h35min de 30 de Setembro de 2007 (UTC)
--Marcos A. N. de Moura 18h35min de 30 de Setembro de 2007 (UTC)
-
 Feito Ok! A parte sobre o infinito poético tinha passado despercebida... Helder 23h50min de 5 de Outubro de 2007 (UTC)
Feito Ok! A parte sobre o infinito poético tinha passado despercebida... Helder 23h50min de 5 de Outubro de 2007 (UTC)
- ==>Bem, seríamos um tanto soberbos em despresar: O infinito filosófico, o infinito poético, o infinito religioso... (Lendo, o início do pensamento sobre infinito você verá o porquê desta expressão)
- "operação inversa"? Não é bem uma operação inversa. Como eu disse acima, analisamos a função nos casos (1) e (2). São casos distintos! E não são inversos um do outro...
- ==>Desculpe, mas não entendi... Naquele caso fazer a tendência a infinito não é fazer o inverso da tendência a zero? --Marcos A. N. de Moura 18h35min de 30 de Setembro de 2007 (UTC)
-
 Concordo parcialmente. Em, certo sentido, é sim. Mas agora que acrescentei algumas coisas na seção, confira se eu ainda mantive o sentido que a troca de "zero" por "infinito" devia ter... acho que está ok!
Concordo parcialmente. Em, certo sentido, é sim. Mas agora que acrescentei algumas coisas na seção, confira se eu ainda mantive o sentido que a troca de "zero" por "infinito" devia ter... acho que está ok! Helder 23h50min de 5 de Outubro de 2007 (UTC)
Helder 23h50min de 5 de Outubro de 2007 (UTC)
- Está correta a expressão "limite lateral positivo no infinito"? Eu nunca vi isso escrito assim... (não seria "limite no infinito positivo")
- ==>De fato, deve ter sido escrito na pressa, já corrigi.
 --Marcos A. N. de Moura 18h35min de 30 de Setembro de 2007 (UTC)
--Marcos A. N. de Moura 18h35min de 30 de Setembro de 2007 (UTC)
-
 Feito Helder 23h50min de 5 de Outubro de 2007 (UTC)
Feito Helder 23h50min de 5 de Outubro de 2007 (UTC)
- ==>De fato, deve ter sido escrito na pressa, já corrigi.
- Não acho que deveríamos dizer que faremos um estudo de "como representá-lo", mas sim um estudo "da função" (afinal o cálculo é feito principalmente para se estudar funções). A função será estudada: (1) quando os valores de x "são muito grandes", ou seja, "tendem ao infinito" (
Sobre a discussão...
Só para encerrar, desculpe se estou fazendo observações demais... só acho que tem coisas que poderiam ser melhoradas no texto (por não estar bem, ou não estar correto, ou mesmo para deixar mais claro), e estou disposto a ajudar nisso! ![]() Mas sinta-se livre pra avisar quando eu exagerar em algum ponto... Um bom fim de semana! Até mais! Helder 22h18min de 29 de Setembro de 2007 (UTC)
Mas sinta-se livre pra avisar quando eu exagerar em algum ponto... Um bom fim de semana! Até mais! Helder 22h18min de 29 de Setembro de 2007 (UTC)
- ==>Fique a vontade, o texto está aí para adaptações, correções e inclusões... A propósito, se tiver vontade pode fazer o resto da subseção sobre continuidade. Porém, acho melhor apenas acrescentar, o que está escrito está num formato didático detalhado não por acaso, foi colocado desta maneira propositalmente para determinar os passos a serem seguidos pelos leitores ao analisarem as funções. --Marcos A. N. de Moura 18h35min de 30 de Setembro de 2007 (UTC)
 Concordo com a idéia de continuar a subseção. Conforme o tempo me permita, farei isso. Tentarei ser preciso e consistente com o restante do livro, para que este não pareça fragmentado em seções com estilos muito diferentes... Helder 12h10min de 6 de Outubro de 2007 (UTC)
Concordo com a idéia de continuar a subseção. Conforme o tempo me permita, farei isso. Tentarei ser preciso e consistente com o restante do livro, para que este não pareça fragmentado em seções com estilos muito diferentes... Helder 12h10min de 6 de Outubro de 2007 (UTC)
Resumindo...
Li mais uma vez a seção sobre infinito e, a partir dos comentários nessa discução, tentei incorporar as diferentes idéias discutidas aqui, de forma que o texto continue tanto intuitivo quanto preciso. Por favor, se algum item não ficou legal, voltemos aqui, e continuamos a editar... Ok? Helder 23h50min de 5 de Outubro de 2007 (UTC)
- Restaurei parte do texto cuja exclusão não foi acordada. Mantenho a idéia de que alterações devem ser feitas no texto original por quem escreveu e que inclusões de novos parágrafos são bem vindas. Acredito que a melhor maneira de mudar um parágrafo é propor e esperar que seja bem aceito. --Marcos A. N. de Moura 02h05min de 7 de Outubro de 2007 (UTC)
Continuidade
Definição
- Sobre minha última alteração:
Durante a leitura, a definição de continuidade não me pareceu clara. Reescrevi o paragrafo, conforme me pareceu mais adequado. Peço desculpas por não passar pela discução antes disso. Foi descuido meu... Permita-me fazer alguns comentários. Os trechos que soaram mais estranho foram: suavemente descritível: não sei por que, mas não está muito legal... discreta variação: em vez de discreta, talvez fosse melhor outro termo... cada valor é precedido de outro menor ou maior: isso eu não entendi... poderia muito bem ser precedido de um valor igual... então não sei se a frase diz muita coisa. O que realmente quis dizer? Aguardo novas sugestões... Helder 22h55min de 27 de Setembro de 2007 (UTC)
- De fato, "suavemente descritível" está um tanto obscuro, que tal: "suavemente delineada"?
- Também, "discreta variação" pode trazer confusão com variação discreta (como em séries e topologias), o que pode sugerir uma variação em termos inteiros, o que não é verdade para este caso. Poderíamos modificar para: "pequena variação", não acha?
- No caso da oração, novamente tenho que concordar, de fato podemos ter valores iguais em um intervalo onde a variação é nula... para este caso podemos incluir esta possibilidade: cada valor é precedido de outro igual,menor ou maior, mas com uma variação muito pequena.
- A idéia desta frase é de levar ao leitor a imagem de que há a real necessidade de existência do valor para a função, seja ele qualquer que seja, ou seja, de que não deve haver indeterminação no meio do segmento da curva.
- Bem, aparte dos questionamentos, gostaria de agradecer pela atenção com que esteve analisando o texto, realmente gostei da maneira com que analisou minunciosamente o mesmo, trazendo melhorias. Obrigado. Gostaria também de lhe expor uma maneira simples para chamar a discussão do conteúdo: para isto podemos usar
{{Em discussão}}, dentro da página onde as mudanças estão sendo propostas, depois que entramos num acordo, retiramos a faixa e implementamos as mudanças conforme acordado. --Marcos A. N. de Moura 23h59min de 27 de Setembro de 2007 (UTC)- Tudo bem então! Vou continuar sendo minuncioso...
- Podemos incluir um daqueles "avisos" de que a wikipedia tem um artigo sobre "funções contínuas" em algum lugar?
- Que tal trocar "a função contínua em um intervalo do seu domínio é suavemente descritível " por "a função contínua em um ponto do seu domínio apresenta variações suaves neste ponto ". O que acha?
- e sobre aquela última parte ("'cada valor é precedido de outro menor ou maior, mas com uma discreta variação"), minha crítica não foi em favor de incluir o terceiro (e último caso). Estariamos sendo redundantes ao fazê-lo!
- O que me diz a respeito da função que a cada irracional associa o próprio irracional e aos racionais associa o zero? Ela é contínua no zero, e só nele. Mas aquela frase parece não se entender muito bem com esse exemplo... Fica meio estranho falar em "um valor precedido de outro"...
- Nada pessoal, não fui com a "cara da famigerada frase"... Helder 20h33min de 28 de Setembro de 2007 (UTC)
- Desculpe Helder, mas este livro tenta ser extremamente simples a princípio, tenho certeza de que ao tentar ler a oração com a visão didática, que um educador tem que manter, entenderá o que esta sendo proposto. O resto devo comentar depois, pois meu filho está precisando de mim agora, até mais.--Marcos A. N. de Moura 14h55min de 29 de Setembro de 2007 (UTC)
- Ok! Compreendo a proposta... Não sei como melhorar a oração (mas tá na ponta da lingua... só não sei o que é ainda...). Se um dia desses me ocorrer uma sugestão sobre ela, volto aqui e comento...
 . Não se apresse em comentar o resto... Até + Helder 22h28min de 29 de Setembro de 2007 (UTC)
. Não se apresse em comentar o resto... Até + Helder 22h28min de 29 de Setembro de 2007 (UTC)
- Ok! Compreendo a proposta... Não sei como melhorar a oração (mas tá na ponta da lingua... só não sei o que é ainda...). Se um dia desses me ocorrer uma sugestão sobre ela, volto aqui e comento...
- Desculpe Helder, mas este livro tenta ser extremamente simples a princípio, tenho certeza de que ao tentar ler a oração com a visão didática, que um educador tem que manter, entenderá o que esta sendo proposto. O resto devo comentar depois, pois meu filho está precisando de mim agora, até mais.--Marcos A. N. de Moura 14h55min de 29 de Setembro de 2007 (UTC)
edição pequena
Olá, estava lendo a definição de continuidade, e o primeiro item me chamou a atenção onde alguem por alguma razão disse que a primeira condição de continuidade é que é necessário que exista o limite naquele ponto (que é verdade), mas "eu acho" que somente e necessário mostrar na primeira condição que os pontos próximos (com uma certa distância delta) de um determinado ponto têm as sua imagem próximas de um certo f(a) (com uma certa distãncia epsilon), e não nos preocuparmos, na primeira condição, o que ocorre com f(x), quando x se torna próximo de a, com x diferente de a. (claro que devemos nos preocuparmos com o limite como estava anteriormente, mas não acho correto definir isso no primeiro instante, perfeito seria nos preocuparmos na terceira condição, ao qual seria perfeito). Trocando 6 por meia dúzia: o que foi mudado é que em vez de requerermos na primeira condição que 0<|x-a|<delta, apenas escrevemos |x-a|<delta, o que muda? não é o simples fato de que x pode ser igual a 'a', mas que f[(a-delta,a+delta)]=(f(a)-epsilon,f(a)+epsilon), e é só isso que importa na continuidade. Pessoal essa é minha humilde opinião, posso estar errado, ou posso estar certo, não quero caçar encrenca com ninguém mudando o que mudei, só quero ajudar. Thiago Marcel 01h02min de 21 de Dezembro de 2008 (UTC)
- Nossa... mil desculpas por não termos respondido antes. Eu nem tinha visto que havia editado/comentado por aqui (estava uma correria para mim no fim do ano passado). Acho que ficou melhor como você escreveu. Aproveitei para fazer alguns ajustes... Helder 23h48min de 17 de agosto de 2009 (UTC)
Fórmulas
Sobre as fórmulas que foram usadas para definir o conceito, não seria melhor usar apenas:
Acrescentando como observação que:
A igualdade acima implica que:está no domínio de
; o limite
existe; os dois valores são iguais
Helder 20h34min de 28 de Setembro de 2007 (UTC)
- A síntese não é requerida aqui, na verdade devemos detalhar mais, acrescentar o trecho que deseja pode ser muito bom para a compreensão, mas reduzir as fórmulas não ajuda, apenas reduz informações.
- Quero reforçar o que já havia dito antes, nas seções acima: Se deseja incluir mais material e melhorar a análise desta seção sobre continuidade, fique a vontade, falta muita coisa aqui. Pode concluir esta seção... Obrigado. --Marcos A. N. de Moura 18h43min de 30 de Setembro de 2007 (UTC)
Uso do "seja"
Tenho uma dúvida sobre o uso deste verbo nos textos de matemática. Há bastante tempo leio frases como "seja x um número real tal que..." e "seja f uma função definida por...". Fiquei um pouco surpreso (ou talvez, senti um certo desconforto por não estar acostumado) ao ver que nestes wikilivros de cálculo (e segundo o Google, algumas páginas na web também o fazem...) tem sido usado "seja um número real x tal que..." e também "seja uma função f definida por...", ou seja, os textos que eu lia usavam "seja" + "nome da coisa" + "propriedades da coisa" e aqui usa-se "seja" + "propriedades da coisa" + "nome da coisa". Dúvidas:
- Ambas as formas estão corretas? (gostaria de perguntar isso a alguem da área de letras, mas no momento não sei de ninguém)
- Caso afirmativo: Seria a primeira forma uma convenção do pessoal que publica textos de matemática? Portanto deve ser seguida (apenas para ser consistente com outros textos)?
- Caso negativo: Devemos alterar as ocorrências da forma "não-correta" nos wikilivros?
OBS: Na verdade eu nunca entendi direito o uso que o pessoal da matemática (estou nesse grupo ![]() ) faz do "seja", mas agora percebi como perguntar algo a respeito...
Helder 09h39min de 31 de Outubro de 2007 (UTC)
) faz do "seja", mas agora percebi como perguntar algo a respeito...
Helder 09h39min de 31 de Outubro de 2007 (UTC)
- O verbo "seja", assim como exposto nos ítens em questão, tem como sinônimos: "crie", "faça", etc... Assumindo a forma imperativa com o objeto ao qual se refere posto logo após seu uso. A gramática não instrui dependência de posição entre o objeto e seu predicativo, faz-se apenas uma resalva quanto a pontuação quando o entendimento é prejudicado. O uso do verbo "seja" é encontrado em diversos livros de matemática tendo objeto e predicativo assumindo ambas as posições, direta ou reversa. A tradição do uso deste verbo é dada pela forma de exposição, a qual instrui "criar entes" para explanar o tema e a linha de raciocínio. --Marcos A. N. de Moura 16h24min de 31 de Outubro de 2007 (UTC)
- Obrigado Marcos! Já está mais claro. Mesmo assim, aproveitei pra pedir uma opinião do Salles... Helder 20h54min de 31 de Outubro de 2007 (UTC)
- Após esta ótima explicação do Marcos, não há muito o que se complementar não...
 Salles Neto
Salles Neto  msg 21h25min de 31 de Outubro de 2007 (UTC)
msg 21h25min de 31 de Outubro de 2007 (UTC)
 Obrigado! --Marcos A. N. de Moura 23h42min de 31 de Outubro de 2007 (UTC)
Obrigado! --Marcos A. N. de Moura 23h42min de 31 de Outubro de 2007 (UTC)
- Grato pelos esclarecimentos. Helder 19h31min de 3 de Novembro de 2007 (UTC)
- Após esta ótima explicação do Marcos, não há muito o que se complementar não...
- Obrigado Marcos! Já está mais claro. Mesmo assim, aproveitei pra pedir uma opinião do Salles... Helder 20h54min de 31 de Outubro de 2007 (UTC)
Limites
Sobre o trecho:
(1) E de forma geral definimos que: Seentão
quando
e sobre os parágrafos que o precedem na seção Definição...
Algumas expressões e alguns símbolos ainda não estão claros, principalmente na parte que destaquei logo acima. Por isso, há algum tempo acrescentei (logo após esta parte) a definição de limite na forma como costumo ver em alguns livros que tratam o assunto:
(2) Afirma-se quesomente quando é válida esta propriedade:
tal que
seguida de outra definição, com a simbologia própria da lógica:
(3)
Mas aqui, acrescento uma outra opção, com menos símbolos:
(4) Dizemos quetem o limite
no ponto
, e escrevemos
, quando vale a seguinte condição: Para cada
, existe um
, de tal forma que
, sempre que
e
Permita-me dizer o que me parece inadequado na versão (1)...
- No começo diz-se "Definimos que". Espera-se, acredito, que depois disso siga alguma expressão (simbólica ou não) que será definida a partir de outras já conhecidas até este ponto do texto. No entanto, não é o que aparece em seguida, pois um dos símbolos (
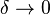 ) não tem qualquer significado ainda.
) não tem qualquer significado ainda. - Parece haver uma "bagunça de símbolos ", pois como se pode ver na versão formal (talvez até d+
 ) (3), o "
) (3), o " " deve estar seguido de uma variável (no caso x).
" deve estar seguido de uma variável (no caso x).
Resumindo, a definição (1) em si não está bem formulada, ou pelo menos poderia estar melhor. Recomendo alterá-la.
Minha sugestão é remover (1) e colocar no lugar (2) ou (4), pois ambas dizem razoavelmente bem o que (1) tenta dizer. Podemos manter (3) por oferecer aos leitores uma comparação entre duas formas bastante diferentes dizer a mesma coisa sendo, portanto, bastante instrutiva...
Quanto ao que vem antes de (1) no texto, não entendi o que se tenta fazer. É alguma "introdução" ao que vai ser dito na definição propriamente dita?
- Se for, acho desnecessário, pois a seção anterior já se presta a este propósito.
- Se não, acho bom revisarmos, pois não ficou claro o que se pretende...
Helder 00h18min de 22 de Novembro de 2007 (UTC)
 A favor Tudo bem, esta parte não estava completa ainda, como boa parte desta página, da mesma forma que a parte de continuidade que foi apenas iniciada. Retiremos a definição simbólica inicial. --Marcos A. N. de Moura 14h15min de 22 de Novembro de 2007 (UTC)
A favor Tudo bem, esta parte não estava completa ainda, como boa parte desta página, da mesma forma que a parte de continuidade que foi apenas iniciada. Retiremos a definição simbólica inicial. --Marcos A. N. de Moura 14h15min de 22 de Novembro de 2007 (UTC)
- Fiz mais uns ajustes na formatação, e eliminei algumas informações que foram ficando repetidas conforme fiz as edições. Agora os últimos parágrafos estão mais "limpos".
- Eu precisei "quebrar" a linha de uma das definições simbólicas, pois em telas com baixa resolução estava ficando feio (ultrapassa a margem direita). Na verdade, eu preferia que o navegador posicionasse automáticamente em uma ou duas linhas, conforme necessário, mas não sei fazer isso sem remover o destaque (a linha começa com "espaço")... Há como simular o efeito de borda e sombra usando alguma outra coisa? Tipo tabela, ou <div> ? Aceito sugestões...Helder 17h13min de 22 de Novembro de 2007 (UTC)
Marcos, acho que ficou pendente seu parecer sobre uma das coisas que perguntei acima. Para ser específico: Quanto a este trecho:
Seja a função 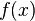 , onde , onde 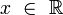 , se , se  é um ponto de acumulação de é um ponto de acumulação de 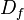 (o domínio de f), existe um número (o domínio de f), existe um número 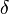 , tal que: , tal que:
e sendo e quando diminuimos |
não entendi o que se tenta fazer. É alguma "introdução" ao que vai ser dito na definição propriamente dita?
- Se for, acho desnecessário, pois a seção anterior já se presta a este propósito.
- Se não, acho bom revisarmos, pois não ficou claro o que se pretende...
Helder 00h18min de 22 de Novembro de 2007 (UTC)
- Helder, eu não sei se estou ficando muito velho, não sei se hoje não se faz mais isto, mas a maneira que eu li em livros que costumava estudar, era introduzir o conceito em partes, explicando o que cada coisa significa e depois sintetizar tudo na fórmula geral. Se não se usa mais isso, todo bem, pode retirar esta parte, caso não ache que está bastante claro, pode tentar melhorar. Mas, se isso não se pratica mais, vou começar a frequentar mais os sebos.
 --Marcos A. N. de Moura 19h19min de 7 de Dezembro de 2008 (UTC)
--Marcos A. N. de Moura 19h19min de 7 de Dezembro de 2008 (UTC)
- Então Marcos, acho que o que você diz continua sendo feito sim, e considero muito importante. É como se, em linhas gerais, a caracterização de um certo conceito novo fosse feita por etapas, partindo de exemplos particulares, depois indicando o que os exemplos têm em comum, e finalizando com a definição propriamente dita. A outra possibilidade é partir de uma definição "abstrata" (ou "geral"), e apresentar instâncias desse conceito abstrato, através de exemplos que tentam mostrar as varias sutilezas da definição. Ainda não pude olhar com calma as modificações que fez, prometo fazê-lo em breve.
- Por hora, gostaria de saber se não prefere reverter a parte desta edição que agora está sob a seção "Definição"? A formatação que eu tinha colocado era para permitir que a expressão (comprida) da definição de limite pudesse ser quebrada em duas linhas caso o leitor use uma tela com pouca resolução. Helder 16h45min de 11 de Dezembro de 2008 (UTC)
- Bem, na minha concepção, o modelo atual me parece bastante adequado, sendo qualquer adição de conteúdo livre e esta modificação foi feita por você, ela fica a seu critério, acho que podemos dar por encerrada a discussão. Ok? --Marcos A. N. de Moura 14h20min de 31 de Dezembro de 2008 (UTC)
- Helder, eu não sei se estou ficando muito velho, não sei se hoje não se faz mais isto, mas a maneira que eu li em livros que costumava estudar, era introduzir o conceito em partes, explicando o que cada coisa significa e depois sintetizar tudo na fórmula geral. Se não se usa mais isso, todo bem, pode retirar esta parte, caso não ache que está bastante claro, pode tentar melhorar. Mas, se isso não se pratica mais, vou começar a frequentar mais os sebos.
Eu ainda gostaria de remover a seção que mencionei. O termo que eu usaria neste caso é que está "mal escrito". Antes que comente, não estou usando a expressão como ofensa, é comum usarmos (pelo menos eu e alguns amigos da matemática) para descrever falhas na lógica de um raciocínio ou uma mistura de símbolos/termos/conceitos em um texto de matemática. No caso daquela seção eu sinceramente achei uma bagunça... =/
Acho que minha tentativa de reescrever foi quando adicionei este trecho. Mas meus motivos para querer apagar a seção (tim tim por tim tim) são os seguintes (senta que la vem a história...rsrs):
- Bom, agora tenho tempo para ler a "história"... As críticas que fez foram muito úteis para o aprimoramento do texto.
- Mas, quanto a remover a seção, não concordo, jamais concordarei, e o motivo é bem simples: Nao expor o tema em detalhes iniciais, simplificados, para depois continuar o texto com mais aprofundamento é uma GIGANTESCA FALHA dos textos em livros de Cálculo que lemos atualmente. Ajustes foram feitos para tentar deixar o texto com melhor qualidade. Espero que você ajude no sentido de aprimorar o texto e não a remover a seção.
Seja a função 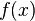 , onde , onde 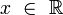 |
Com isso você quer dizer que o domínio de f é a reta toda?
- Se for, então todo ponto a é ponto de acumulação e a hipótese seguinte "se
 é um ponto de acumulação de
é um ponto de acumulação de 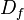 (o domínio de f)" está sobrando.
(o domínio de f)" está sobrando. - Se não for isso o que quer dizer, então "onde
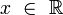 " está sobrando.
" está sobrando.
se  é um ponto de acumulação de é um ponto de acumulação de 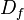 (o domínio de f), existe um número (o domínio de f), existe um número 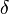 , tal que: , tal que:
|
Na verdade, se a é um ponto de acumulação de D_f, então para todo (em vez de existe) delta existe x em D_f tal que a desigualdade vale. Mas se o domínio de f for a reta toda, todo ponto é ponto de acumulação. Então a desigualdade vale sempre (e portanto está sobrando).
- Reescrevi o texto, pois há certo tempo atrás, ele era apenas um esboço e depois foram incluindo texto sem que eu percebesse e no final ficou uma coisa totalmente fora do que eu tinha imaginado. --Marcos A. N. de Moura (Discussão) 15h04min de 10 de Janeiro de 2010 (UTC)
Sob estas condições, queremos definir o valor de forma que o mesmo seja extremamente pequeno, por isso é importante notar que precisa-se fazer com que  diminua sob a óptica da análise que deveremos fazer. diminua sob a óptica da análise que deveremos fazer. |
Queremos definir o valor de quem? Este parágrafo não estaria querendo dizer o mesmo que "Se \delta é um número pequeno e |x-a|<\delta então x está próximo de a ;" que aparece antes desta seção? Se sim, está sobrando. Se não, mal escrito.
- Foi reescrito. Como já havia dito, isso era apenas um esboço... --Marcos A. N. de Moura (Discussão) 15h04min de 10 de Janeiro de 2010 (UTC)
Sendo 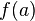 , definido ou não, ... , definido ou não, ... |
Se não me engano, não tem essa de "f(a) definido ou não". O símbolo f(a) é usado para indicar o valor de f no ponto a, então só pode ser usado quando a f está definida em tal ponto.
- Oops, aqui foi erro de digitação mesmo, quis dizer que f(x) pode estar indefinido, apoiando a segunda condição de continuidade que exige que função exista. Isso admite a possibilidade de que ela não exista. --Marcos A. N. de Moura (Discussão) 15h04min de 10 de Janeiro de 2010 (UTC)
...verificamos a existência de um número que tende a  |
Números não tendem, o que tendem são sequências (de números, funções, ...)
- Bem, aqui o formalismo fala mais alto, concordo que pode ser melhorado e já ajustei. --Marcos A. N. de Moura (Discussão) 15h04min de 10 de Janeiro de 2010 (UTC)
e que exista um número  , , |
Nas definições de limites, geralmente o quantificador com o epsilon é o "para todo", pois se quer dizer que para todo intervalo aberto do contradomínio vale certa coisa (que é a existência de um intervalo aberto no domínio com certas propriedades...). Parece estar sendo feito um mal uso dos quantificadores (pois la em cima foi trocado o existe e aqui o para todo).
- A respeito do formalismo, fiz a modificação do texto apenas para simplificá-lo. Realmente não tenho desejo nenhum de tornar esta seção formalmente rebuscada. E, para falar a verdade, tenho verdadeiro horror a textos que primam pela elegância apenas para mostrar que o autor conhece o tema. Seria bom que todos possibilitassem que pessoas que procuram entender tenham o acesso ao conhecimento de forma mais simples. --Marcos A. N. de Moura (Discussão) 15h04min de 10 de Janeiro de 2010 (UTC)
Quando diminuimos 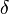 até que não seja mais possível distingüir até que não seja mais possível distingüir  de de  ,embora eles sejam infinitesimalmente diferentes, deveremos ter um ,embora eles sejam infinitesimalmente diferentes, deveremos ter um  correspondente. correspondente. |
"devemos ter um epsilon correspondente"? Novamente a troca de papeis entre as letras epsilon e delta: é dado um epsilon arbitrário e para cada um deles existe um delta correspondente (e não o contrário).
- Isto quer dizer que, se eu inverter o sentido da análise, diferente do que se vê em textos atuais eu estou fazendo a análise de forma incorreta? Tenho certeza que não, pois tenho esse tipo de análise em livros mais antigos que li, mas mesmo assim modificarei o texto para acabar com isso logo. --Marcos A. N. de Moura (Discussão) 15h04min de 10 de Janeiro de 2010 (UTC)
Depois de alguns erros ou imprecisões, não dá para dar sentido a frase
Caso isto seja possível,  é o limite de é o limite de 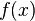 quando quando  tende a tende a  . . |
pelo menos não antes de corrigir os parágrafos precedentes, aos quais o "isto" se refere...
Desculpa a trabalheira com esta seção Marcos... Ela foi realmente difícil de engolir... rsrs Helder 01h16min de 18 de agosto de 2009 (UTC)
- O que tenho a dizer é que as edições feitas depois de um certo tempo descaracterizaram totalmente o que eu pretendia explanar. A seção originalmente era assim. Irei reescrever esta parte de forma mais clara e didática. Porque sob minha óptica, isso foi uma alteração muito grosseira. --Marcos A. N. de Moura (Discussão) 00h02min de 10 de Janeiro de 2010 (UTC)
Propriedades dos limites
- Estive trocando algumas ocorrências de variáveis no meio do texto por códigos em Latex (por exemplo x, foi trocado por
 ), para que a fonte usada em expressões matemáticas ficasse uniforme. Tenho uma dúvida: é melhor usar <math>x</math> ou <math>x\,\! </math> (
), para que a fonte usada em expressões matemáticas ficasse uniforme. Tenho uma dúvida: é melhor usar <math>x</math> ou <math>x\,\! </math> ( ou
ou  ) nas expressões em latex? Não percebi diferença no resultado (além de usar mais caracteres no último caso)...
) nas expressões em latex? Não percebi diferença no resultado (além de usar mais caracteres no último caso)...
- Dependendo do navegador e suas preferências pessoais, se você escolher que as fórmulas sejam mostradas sempre em latex, você não perceberá a diferença. Mas, o ideal, é que se use <math>x\,\! </math>, porque as fórmulas sempre aparecerão na fonte do latex, se você não forçar latex com \,\! elas serão enviadas em html, o que não garante a uniformidade do texto.
- Andei corrigindo algumas coisas nas demonstrações das propriedades de limites.
Vou procurar uma demonstração para a propriedade do limite do quociente de funções, e adicionar ao texto (mas estou com uma preguiça de digitá-la em latex...![]() )
)
- Estou pensando em adaptar a demonstração da propriedade de potências de limites para uma prova por indução. O que acha?
- + Uma última coisa, a faixa de discussão pode ser movida para as últimas seções, depois que decidirmos sobre o começo da seção "Definição" de limites?
Helder 13h17min de 28 de Novembro de 2007 (UTC)
- Eu havia imaginado que a predefinição para sugestão de aprimoramento deveria ser colocada em cada seção a ser discutida. --Marcos A. N. de Moura (Discussão) 16h29min de 10 de Janeiro de 2010 (UTC)
- Bem, nada contra em mudar a demonstração, na verdade é melhor a versão mais científica.
- Quanto a faixa, acho que deveríamos resolver logo tudo e retirar a faixa, pois a em síntese a faixa significa que o material está sendo posto em dúvida quanto a sua validade. --Marcos A. N. de Moura 15h04min de 7 de Dezembro de 2008 (UTC)
- Citação: Helder escreveu: «Vou procurar uma demonstração para a propriedade do limite do quociente de funções» Boa sorte, porque esta demonstração non ecziste. Só existe no caso em que o limite do denominador seja diferente de zero :-) Aliás, estes teoremas T1 a T6 deviam vir precedidos de "Suponha que os limites de f(x) e g(x) existem. Então..." Albmont (Discussão) 01h06min de 10 de Janeiro de 2010 (UTC)
- Incluído... --Marcos A. N. de Moura (Discussão) 16h29min de 10 de Janeiro de 2010 (UTC)
- Citação: Helder escreveu: «Vou procurar uma demonstração para a propriedade do limite do quociente de funções» Boa sorte, porque esta demonstração non ecziste. Só existe no caso em que o limite do denominador seja diferente de zero :-) Aliás, estes teoremas T1 a T6 deviam vir precedidos de "Suponha que os limites de f(x) e g(x) existem. Então..." Albmont (Discussão) 01h06min de 10 de Janeiro de 2010 (UTC)
teorema do confronto
Por quê faltou falar do teorema do confronto/valor médio ? seria interessante colocá-lo com as demais propriedades do limite, como T7, por exemplo
O histórico anterior da página foi arquivado para fins de backup em Discussão:Cálculo (Volume 1)/Limites e Continuidade/Arquivo LQT 1 em 2015-11-03.
 , quando
, quando  é muito grande?
é muito grande? , os valores de
, os valores de  , embora, naturalmente, existam inúmeras funções que aumentam seus valor conforme
, embora, naturalmente, existam inúmeras funções que aumentam seus valor conforme 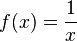 , pois assim evitamos um comportamento diferente para números negativos próximos de zero.
, pois assim evitamos um comportamento diferente para números negativos próximos de zero.
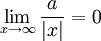
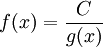
 forneça valores menores que 1. Obviamente existem inúmeras formas de criar funções que aumentam seu valor sucessivamente, usaremos esta pois nos ajuda a eliminar números racionais que nos trazem mais dificuldades na análise dos resultados, como veremos logo adiante.
forneça valores menores que 1. Obviamente existem inúmeras formas de criar funções que aumentam seu valor sucessivamente, usaremos esta pois nos ajuda a eliminar números racionais que nos trazem mais dificuldades na análise dos resultados, como veremos logo adiante. 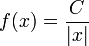
 forneça valores que diminuem até zero. É importante notar que quanto mais
forneça valores que diminuem até zero. É importante notar que quanto mais  diminui, mais os valores da função
diminui, mais os valores da função  ) e (2) quando a função "cresce muito", "tendendo ao infinito" se aproximamos x de um certo ponto (
) e (2) quando a função "cresce muito", "tendendo ao infinito" se aproximamos x de um certo ponto (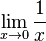 )
)
 ;
o limite
;
o limite 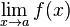 existe;
os dois valores são iguais
existe;
os dois valores são iguais então
então 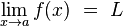 quando
quando 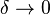
 tal que
tal que 

 , existe um
, existe um  , de tal forma que
, de tal forma que  , sempre que
, sempre que  e
e 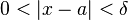
 " deve estar seguido de uma variável (no caso x).
" deve estar seguido de uma variável (no caso x).