Matemática elementar/Funções
Uma função é uma relação especial, que é definida da seguinte maneira: sejam dois conjuntos A e B, tais que para todo elemento x pertencente a A, haja uma correspondência de um elemento y pertencente a B. Essa correspondência é a função: a associação, definida de algum modo, entre todos os elementos de um conjunto e os elementos de outro conjunto.
A função que associa um elemento x a outro valor pode ser indicada por f(x). O aparecimento de x na simbologia da função não ocorre por acaso, uma vez que o valor f(x) depende de x. Por isso mesmo, x é chamada variável independente e f(x) (ou y) é chamada de variável dependente. Matematicamente a função é definida:
- , ou mais simplificadamente,
Um exemplo de função: dado o conjunto dos números naturais, uma função pode associar cada número ao seu quadrado. Assim, essa função assumiria os valores: { 1,4,9,16,... }.
Uma função pode, na verdade, associar mais de um conjunto a outro; pode haver diversas variáveis independentes. Por exemplo: uma função pode tomar dois valores inteiros e expressar sua soma:
No entanto, neste livro será dada mais atenção às funções de uma variável, apenas. São duas características da função enquanto relação:
- há correspondência unívoca entre um elemento e o valor associado a ele pela função: isso significa que para cada valor assumido pela variável independente (x), há um único valor da variável dependente (y) associado pela função. Consequentemente, se t = f(x) e w = f(x), então t = w.
- a correspondência é total, ou seja, um valor assumido pela variável dependente estará associado para todo valor possível de ser assumido pela variável independente.
A tabela a seguir mostra dois exemplos de relações que não são funções:

|

|
| Nesse caso, um mesmo elemento (3) do domínio X aparece associado a dois elementos do contradomínio Y (c,d). | Aqui a correspondência não é total: falta um valor associado a 1. |
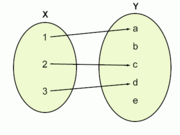
Já o diagrama a seguir representa uma função:
Duas funções f e g são ditas iguais (f = g) se e somente se para cada valor de x no domínio D, f(x) e g(x) assumam o mesmo valor:
- OBS.: uma função é uma relação, por isso não possui grau. Quem possui grau são os polinômios associados a função. Dessa maneira é um equívoco pensar em "função de 1° ou 2° graus".
Introdução
editarRelações que estabeleçam dependência entre os elementos de dois conjuntos são denominadas funções.
Um exemplo clássico de função é a do salário de vendedores que ganham por comissão:
Existe um valor fixo que o vendedor ganha mesmo se não conseguir vender nada naquele mês e uma comissão, que depende da quantidade de vendas que o vendedor realizou. Por exemplo:
| Vendas | Comissão por venda | Valor Fixo | Salário |
| 0 | 55 | 300 | 300 |
| 1 | 55 | 300 | 355 |
| 2 | 55 | 300 | 410 |
| ... | ... | ... | ... |
Da tabela acima podemos construir uma relação entre as vendas e o salário do vendedor:
E com isso, construímos um gráfico que relaciona vendas a salário, onde verifica-se que:
- O salário depende das vendas.
- O salário é uma função das vendas.
Definição
editarAo aplicar uma função em um dado conjunto , cada elemento deste deverá ter como correspondente um elemento em um dado conjunto .
Ao conjunto denomina-se domínio da função, sendo seus elementos denominados abscissas, e ao conjunto denomina-se contra-domínio, sendo seus elementos denominados ordenadas ou imagens, quando estas se correlacionarem a um elemento de .
Ou seja:
Dados dois conjuntos e não vazios, dizemos que a relação f de em será função se, e somente se,
- .
(Para qualquer x pertencente a D existe um y pertencente a C tal que o par ordenado (x,y) pertence à função f)
- Obs: Para cada , deve haver apenas um
Representações
editarExistem várias maneiras de se representar funções.
Abaixo você pode ver as três mais comumente utilizadas, sendo a primeira a predominante.
As representações abaixo são de uma função em relação a seu domínio e contra-domínio.
Há também as representações por sua fórmula algébrica em relação a sua imagem, como a seguir:
Condições de existência
editarAs condições básicas de existência são:
- Todo e qualquer elemento do domínio deve possuir uma única imagem no contra-Domínio.
- Caso a equação algébrica da função contenha uma fração, seu denominador deve ser diferente a 0 (zero).
- Caso a equação algébrica da função possua uma raíz de índice par, para que seu resultado pertença aos Reais, o radicando deve ser maior ou igual a 0 (zero).
- Caso essa mesma raíz esteja no denominador de uma fração, o radicando deve ser estritamente maior que 0 (zero).
- Caso o índice dessa raíz seja um número ímpar, a única restrição é que o radicando seja diferente de 0 (zero).
Com isso, cada função deverá ter suas restrições particulares, mas sempre obedecendo as gerais acima. Algumas regras não são aplicáveis a funções com contradomínio Complexo.
Nomenclaturas
editarAbaixo você confere o que significa cada nome utilizado ao se falar sobre funções:
Domínio, contradomínio e imagem
editarSão três conjuntos especiais associados à função. O domínio é o conjunto A do exemplo dado no início deste capítulo: contém todos os elementos x para os quais a função deve ser definida. Já o conjunto B do exemplo é o contradomínio: o conjunto que contém os elementos que podem ser relacionados a elementos do domínio.
Também define-se o conjunto imagem como o conjunto de valores que efetivamente f(x) assume. O conjunto imagem é, pois, sempre um subconjunto do contradomínio.
Por exemplo, suponha a função que associa um elemento do domínio D = { 1,2,3,4,5 } a uma vogal ordenada no alfabeto.
- O domínio, já especificado, é
- O contradomínio é
- A imagem é
Gráfico Cartesiano
editar- Abscissa
- Todo e qualquer elemento do domínio.
- Ordenada
- Todo e qualquer elemento do conjunto imagem.
- Gráfico em Plano Cartesiano da função
- Representação de todos os pontos que compõem uma função através de dois eixos perpendiculares.
Funções Sobrejetoras, Injetoras e Bijetoras
editarFunções Pares e Ímpares
editar- Uma função é denominada par quando , para todo (domínio de f).
- Uma função é denominada ímpar quando , para todo .
Propriedades das funções
editarContinuidade
editarUma função é dita contínua sobre um intervalo dado, , se possui um valor definido para todos os números contidos nesse intervalo. Por exemplo, a função:
- , definida para o contradomínio , não é contínua no intervalo , uma vez que não está definida para x < 0.
Crescimento e decrescimento
editarUma função é dita crescente, sobre um intervalo [A,B], se para cada valor de x + ε (ε sendo qualquer valor positivo), .
Uma função é dita decrescente, sobre um intervalo [A,B], se para cada valor de x + ε (ε sendo qualquer valor positivo), .
Paridade
editarA paridade de uma função é uma propriedade relacionada a simetria da mesma, e portanto só pode ser definida para funções cujo domínio é simétrico (veja a definição de conjunto simétrico). Sendo um elemento pertencente a um conjunto simétrico , uma função é dita:
- par, se para todo , ; ou seja, o valor da função é definido apenas de acordo com o módulo da variável independente;
- ímpar, se para todo , ;
- sem paridade, se não corresponder a nenhum dos dois casos anteriores.
Funções polinomiais de primeiro e segundo graus
editarExistem dois tipos especiais de funções a respeito das quais cabe fazer comentários aqui. Uma função é dita polinomial do primeiro grau ou afim quando pode ser expressa na forma:
A função polinomial do primeiro grau sempre toma no gráfico a forma de pontos colineares. Se o domínio da função for o conjunto R, tem-se uma reta.
O valor da constante , na função e que tem domínio igual a , é chamado coeficiente angular da reta que define a função. Ele pode ser obtido a partir da relação entre quaisquer dois pontos da reta (ou valores associados da variável independente e dependente), conforme a equação:
Para o caso específico da constante ser igual a zero, a função é chamada função linear.
.
Já a função do segundo grau toma a forma:
Graficamente, a função do segundo grau é sempre uma parábola, cuja concavidade depende unicamente do sinal da constante a. Se a for negativo, a parábola tem o vértice voltado "para cima"; se a for positivo, a parábola tem o vértice voltado "para baixo". (Considerando a representação usual do plano cartesiano.)
Operações sobre funções
editarSoma, produto e quociente
editarComposição de funções
editarO conceito de uma função é uma generalização da noção comum de "fórmula matemática". Funções descrevem relações matemáticas entre dois objetos, e . O objeto é chamado o argumento da função , e o objeto , que depende de , é chamado imagem de pela .
Intuitivamente, uma função é uma maneira de associar a cada valor do argumento um único valor da função . Isto pode ser feito especificando através de uma fórmula ou regra de associação, um gráfico, ou uma simples tabela de correspondência...
Alguns tipos de funções
editarPropriedades fundamentais, gráficos, máximos, mínimos, equações e inequações envolvendo estas funções.