Matemática elementar/Imprimir
Conjuntos
editarEm Matemática, conjunto é uma coleção de objetos (chamados elementos). Os elementos podem representar qualquer coisa — números, pessoas, letras, etc - até mesmo outros conjuntos. Um conjunto pode conter outro(s) conjunto(s), inclusive. Incorretamente chamada de "Teoria dos Conjuntos" no ensino médio. Essa teoria existe, mas não é tratada no ensino médio, sendo a Teoria mais conhecida, a Axiomática de Zermello Frankel (ZFC, C relacionado ao Axioma da Escolha), tratada de forma elementar no livro "Teoria Ingênua dos Conjuntos" de Paul Halmos, traduzida para o português pelo prof. Irineu Bicudo.
Trata-se de um conceito primitivo. Um conjunto possui como única propriedade os elementos que contém. Ou seja, dois conjuntos são iguais se eles tem os mesmos elementos.
Representação
editar
Matematicamente o conjunto é representado por uma letra do alfabeto latino, maiúscula (A, B, C, ...). Já os elementos do conjunto são representados por letras latinas minúsculas. E a representação completa do conjunto envolve a colocação dos elementos entre chaves, da seguinte maneira:
Para um conjunto A de 4 elementos v, x, y e z
A exceção é feita a conjuntos que contenham elementos que devem ser representados por letras maiúsculas — por exemplo, pontos geométricos:
Especificando conjuntos
editarA maneira mais simples de representar algebricamente um conjunto é através de uma lista de seus elementos entre chaves ({ }), conforme descrito nas seções anteriores:
Informalmente, usa-se o sinal ... quando a regra de formação do conjunto é óbvia a partir da enumeração de alguns elementos. Por exemplo, os conjuntos abaixo, o primeiro com um número finito, e o segundo com um número infinito de elementos:
Conjuntos que são elementos de outros conjuntos são representados com chaves dentro de chaves:
Porém há notações alternativas para representar os conjuntos, como a chamada notação de composição do conjunto, que utiliza uma condição P para definir os elementos do conjunto:
P é uma função na variável x que tem o domínio igual ao conjunto A. A variável x pode estar limitada por outro conjunto, indicando-se a relação de pertinência adequada. Por exemplo:
O conjunto A será formado, de acordo com o desenvolvimento da equação dada, por 2 e 4 (únicos números inteiros que satisfazem a condição P, ou seja, que tornam verdadeira a equação). Logo, .
Um cuidado deve ser tomado com a propriedade P(x), já que a formação de conjuntos através deste método pode gerar resultados paradoxais.
Terminologia
editarConjunto unitário
editarUm conjunto unitário possui um único elemento.
Conjunto vazio
editarTodo conjunto também possui como subconjunto o conjunto vazio representado por , , ou .[1] Podemos mostrar isto supondo que se o conjunto vazio não está contido no conjunto em questão, então o conjunto vazio deve possuir um elemento ao menos que não pertença a este conjunto. Como o conjunto vazio não possui elementos, isto não é possível. Como todos os conjuntos vazios são iguais uns aos outros, é permissível falar de um único conjunto sem elementos.
Subconjuntos
editar
Dizemos que um conjunto A é subconjunto de outro conjunto B quando todos os elementos de A também pertencem a B. Por exemplo:
- A = { 1,2,3 }
- B = { 1,2,3,4,5,6 }
Nesse caso A é subconjunto de B, é indica-se . Deve-se reparar que B é subconjunto de si mesmo; os subconjuntos de B que não são iguais a B são chamados subconjuntos próprios.
Nota: O conjunto vazio, { } ou Ф (phi), é um subconjunto de todos os conjuntos.
Conjunto das partes ou potência
editarDado um conjunto A, definimos o conjunto das partes de A, , como o conjunto que contém todos os subconjuntos de A (incluindo o conjunto vazio e o próprio conjunto A).
Uma maneira prática de determinar é pensar em todos os subconjuntos com um elemento, depois todos os subconjuntos com dois elementos, e assim por diante.
Exemplo:
- Se A = { 1, 2, 3 }, então = { ∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} }.
Observação:
- Se o conjunto A tem n elementos, o conjunto terá 2n elementos. Ou seja:
- .
Demonstração: Seja P(A) o conjunto de partes de A e n(S) o número de elementos distintos de S.
Se A = → P(A) = {} → n(P(A)) = 2^0 = 1
Se A = {a} → P(A) = {,a} → n(P(A)) = 2^1 = 2
Se A = {a,b} → P(A) = {,a,b,{a,b} → n(P(A)) = 2^2 = 4
Se A = {a,b,c} → P(A) = {,a,b,c,{a,b},{b,c},{a,c},{a,b,c}} → n(P(A)) = 2^3 = 8
...
P(A) é formado por somado às possíveis combinações dos elementos de A, com taxa variando de 1 a n(A).
Assim, n(P(A)) = número de combinações n(A), com taxa variando de 1 a n(A) somado a 1 (responsável por ).
n(P(A)) =
Pelo triângulo de pascal, com a soma das linhas:
→ n(P(A)) =
Mas,
→ n(P(A))
Provando, portanto, que o número de elementos do conjunto de partes de A é dois elevado ao número de elementos distintos de A.
Nota: O conjunto das partes é uma álgebra booleana sobre as operações de união e interseção.
O Teorema de Cantor estabelece que .
Conjunto Universo
editarEm certos problemas da teoria dos conjuntos, é preciso que se defina um conjunto que contenha todos os conjuntos considerados. Assim, todos os conjuntos trabalhados no problema seriam subconjuntos de um conjunto maior, que é conhecido como conjunto universo, ou simplesmente universo.
Por exemplo: em um problema envolvendo conjuntos de números inteiros, o conjunto dos números inteiros Z é o conjunto universo; em um problema envolvendo palavras (consideradas como conjuntos de letras), o universo é o alfabeto.
Relações entre conjuntos
editarRelação de inclusão
editarPara relacionar um conjunto com outro conjunto(ou subconjunto) utilizamos a relação de inclusão.
Exemplo: Se considerarmos o conjunto formado por todas as letras do alfabeto e o conjunto formado pelas vogais, podemos dizer que (A contém V) ou (V está contido em A)
Relação de pertinência
editarSe é um elemento de , nós podemos dizer que o elemento pertence ao conjunto e podemos escrever . Se não é um elemento de , nós podemos dizer que o elemento não pertence ao conjunto e podemos escrever .
Exemplos:
Subconjuntos próprios e impróprios
editarSe e são conjuntos e todo o elemento pertencente a também pertence a , então o conjunto é dito um subconjunto do conjunto , denotado por . Note que esta definição inclui o caso em que e possuem os mesmos elementos, isto é, são o mesmo conjunto (). Se e ao menos um elemento pertencente a não pertence a , então é chamado de subconjunto próprio de , denotado por . Todo conjunto é subconjunto dele próprio, chamado de subconjunto impróprio.
Igualdade de conjuntos
editarDois conjuntos A e B são ditos iguais se, e somente se, têm os mesmos elementos. Ou seja, todo elemento de A é elemento de B e vice-versa. A simbologia usada é . Se um conjunto não é igual a outro, utiliza-se o símbolo .
Simetria de conjuntos
editarUm conjunto A é dito simétrico se, para todo elemento a pertencente a ele, houver também um elemento -a pertencente a esse conjunto. Os conjuntos numéricos Z, R, Q e C são simétricos.
Operações com conjuntos
editar
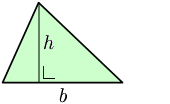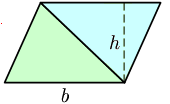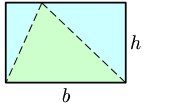
- A união de dois conjuntos A e B é um conjunto que contém todos os elementos de A, todos os elementos de B, e nada mais além disso. Ou então: Dado um universo U e dois conjuntos A e B, chama-se união de A co|A união de dois conjuntos A e B é um conjunto que contém todos os elementos de A, todos os elementos de B, e nada mais além disso. Ou então: Dado um universo U e dois conjuntos A e B, chama-se união de A co m B ao conjunto cujos elementos pertencem pelo menos ao conjunto A ou ao conjunto B. Matematicamente:
Por exemplo:
Observar no último exemplo que os elementos repetidos (3,5) não aparecem na união.
- A união de um conjunto , qualquer que seja, com o conjunto vazio é igual ao próprio conjunto , .
- Também deve ser observado que a operação de união é comutativa, ou seja, .
Intersecção
editar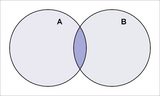
A intersecção de dois conjuntos e , é o conjunto de elementos que pertencem aos dois conjuntos. Ou então: Dados dois conjuntos e , pertencentes a um universo U, chama-se intersecção de A com B ao conjunto cujos elementos pertencem tanto a quanto a . Matematicamente:
Por exemplo:
Observar no último exemplo que, dado os conjuntos não terem elementos iguais, a intersecção resulta num conjunto vazio.
Diferença
editar
Dado um universo U ao qual pertencem dois conjuntos A e B, chama-se diferença de A menos B ao conjunto de elementos que pertencem a A e não pertencem a B; chama-se de diferença de B menos A ao conjunto de elementos que pertencem a B e não pertencem a A. Matematicamente:
Por exemplo, o conjunto definido pela diferença entre os números inteiros e números naturais é igual ao conjunto Z- (números inteiros não-positivos):
- Z = {...,-2,-1,0,1,2,...}
- N = {1,2,3,4,5,...}
- A subtração de um conjunto A menos um conjunto vazio é igual ao próprio conjunto A, .
Complementar
editar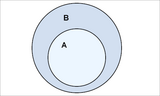
Dado um universo U, diz-se complementar de um conjunto A, em relação ao universo U, o conjunto que contém todos os elementos presentes no universo e que não pertençam a A. Também define-se complementar para dois conjuntos, contanto que um deles seja subconjunto do outro. Nesse caso, diz-se, por exemplo, complementar de B em relação a A (sendo B um subconjunto de A) — é o complementar relativo — e usa-se o símbolo . Matematicamente:
Exemplo:
- A = { 3,4,9,{10,12},{25,27} }
- D = { {10,12} }
Cardinalidade
editarA cardinalidade de um conjunto A representa a quantidade de elementos do conjunto, e é
Exemplos:
- Se A = { 7, 8, 9 }, então a cardinalidade do conjunto A é 3.
- Se A = { }, então a cardinalidade do conjunto A é 0.
Se um conjunto tem n elementos, onde n é um número natural (possivelmente 0), então diz-se que o conjunto é um conjunto finito com uma cardinalidade de n ou número Número cardinal n.
Mesmo se o conjunto não possui um número finito de elementos, pode-se definir a cardinalidade, graças ao trabalho desenvolvido pelo matemático Georg Cantor. Neste caso, a cardinalidade poderá ser (aleph zero), .
Nos dois casos a cardinalidade de um conjunto é denotada por ou por . Se para dois conjuntos A e B é possível fazer uma relação um-a-um (ou seja, uma bijeção) entre seus elementos, então .
Problemas matemáticos sobre cardinalidade
editarOs problemas matemáticos no nível elementar sobre cardinalidade usualmente tomam as formas seguintes:
- É dada a cardinalidade de alguns conjuntos e suas interseções, uniões ou diferenças, e pede-se a cardinalidade de algum conjunto derivado dele
- É dada a proporção ou porcentagem de alguns subconjuntos de algum conjunto (universo), e pede-se este número para outro subconjunto.
Um problema típico simples do primeiro caso é:
- Em uma escola, existem duas atividades extra-escolares: Artesanato ou Bioterrorismo. 59 alunos fazem Artesananto, 87 alunos fazem Bioterrorismo, e 31 alunos fazem ambos. Quantos alunos fazem alguma atividade extra?
Um problema típico simples do segundo caso é:
- Em uma cidade, 5% da população foi exposta ao Antrax, 8% da população foi exposta a Peste Bubônica, e 87% da população não foi exposta a Antrax nem Peste Bubônica. Quantas pessoas foram expostas a Antrax e Peste Bubônica?
A resolução, nos dois casos, deve ser feita com o Diagrama de Venn, marcando-se em cada pedaço o número (ou porcentagem) de elementos, começando-se sempre do mais interno para o mais externo. No caso da porcentagem, deve-se levar em conta que o total do Universo é 100%.
Exercícios
editarPar ordenado
editarUm par ordenado é uma coleção de dois objetos que tem uma ordem definida; existe o primeiro elemento (ou primeira coordenada) e o segundo elemento (ou segunda coordenada). Diferentemente do conjunto { a,b }, um par ordenado — simbolizado por (a,b) — precisa ser apresentado em uma determinada ordem, e dois pares ordenados só são iguais quando os primeiros elementos são iguais e os segundos elementos são iguais. Ou seja,
Porém, o par ordenado pode ser representado como um conjunto, tal que não existe ambiguidade quanto à ordem. Esse conjunto é:
Observar que o formato do conjunto, que inclui um subconjunto contendo os dois elementos do par e um conjunto contendo o primeiro elemento, elimina a possibilidade de ambiguidade quanto à ordem. A notação (a,b) também é conhecida como intervalo aberto.
Produto cartesiano
editarDados dois conjuntos A e B, chama-se produto cartesiano de A em B ao conjunto formado por todos os pares ordenados cuja primeira coordenada seja pertencente a A, e a segunda coordenada seja pertencente a B. O símbolo do produto cartesiano é . Matematicamente:
O produto cartesiano de dois conjuntos A e B é o conjunto de pares ordenados:
A soma ou união disjunta de dois conjuntos A e B é o conjunto
- .
- O produto cartesiano é não-comutativo: .
- Quem desenvolveu o conceito de produto cartesiano foi o matemático Descartes, quando desenvolvia a geometria analítica. Ele enunciou, por exemplo, que o produto cartesiano definido por dois conjuntos de números reais R (imagine os eixos das abcissas e ordenadas num gráfico) é igual a um plano.
Relações
editarNa teoria dos conjuntos, qualquer subconjunto do produto cartesiano A × B é chamada relação de A em B. (O assunto é abordado com mais detalhes na próxima seção.)
Notas
editar- ↑ Estas notações foram introduzidas pelo grupo Bourbaki, que inspirou-se na letra norueguesa Ø.
Ver também
editarWikilivros
editar- Teoria dos conjuntos - texto mais avançado
Wikipédia
editarLigações externas
editar- Números Naturais: Primeira parte
- Números Naturais: Segunda parte
- Critérios de Divisibilidade
- Exercícios Resolvidos de MDC, MMC e Divisores
- Números Inteiros
- Frações
- Frações e Números Decimais
- Números Racionais
- Frações e Números decimais (Exercícios)
Números naturais
editarDefinição
editarUm número natural é um número inteiro não-negativo (0, 1, 2, ...). Em alguns contextos, o número natural é definido como um número inteiro positivo, i.e., o zero não é considerado como um número natural. O uso mais comum deles é a contagem ou a ordenação. As propriedades dos números naturais como, por exemplo, divisibilidade e a distribuição dos números primos, são estudadas neste capítulo. Outras propriedades que dizem respeito a contagens e combinações são estudadas pela análise combinatória.
Os matemáticos usam para se referir ao conjunto de todos os números naturais. Este conjunto é infinito e contável por definição.
= {0,1,2,3,4,5,6,7,...}
Se retirarmos o desses conjunto, obtemos o subconjunto:
= {1,2,3,4,5,6,7,...}
Operações em
editarSão duas as operações em naturais que sempre tem correspondente natural. São a adição e a multiplicação de naturais. As outras operações básicas, a subtração e a divisão nem sempre tem correspondente em naturais, embora possam ter em outros conjuntos.
Por exemplo: 10 e 11 são números naturais, porém, , e não é um número natural. Porém, é um número inteiro, pertencente ao conjunto
Critérios de divisibilidade
editarDivisibilidade por 2
editarUm número é divisível por 2 quando termina em 0, 2, 4, 6 ou 8, isto é, quando é par. Por exemplo, 40, 42, e 44 são números divisíveis por 2.
Divisibilidade por 3
editarUm número é divisível por 3 quando a soma dos valores absolutos de seus algarismos for divisível por 3.
Exemplo:
- 360 (3+6+0=9) → é divisível.
Divisibilidade por 4
editarUm número é divisível por 4 quando os dois últimos algarismo forem 0 ou formarem um número divisível por 4.
Exemplo:
- 416 (últimos dois algarismos: 16 [= 4×4]) → é divisível.
Divisibilidade por 5
editarUm número é divisível por 5 quando termina em 0 ou 5.
Exemplo:
- 2.654.820 → é divisível.
Divisibilidade por 6
editarUm número é divisível por 6 quando é divisível por 2 e por 3.
Exemplo:
- 414 → divisível por 6, pois
- par → divisível por 2
- 4+1+4=9 → divisível por 3.
Divisibilidade por 7
editarA divisibilidade por também pode ser verificada da seguinte maneira:
Tome por exemplo o número 453. Separando-se o último algarismo ficamos com 45 e 3. Do primeiro subtraímos o dobro do segundo, ou seja, Como 39 não é divisível por 7 o número 453 também não é.
Outro exemplo: → Separando e teremos Como é divisível por o número também é.
Outro critério usa a soma e não a subtração. Um número de mais de três algarismos ABCD... é divisível por 7 quando o número B(C+2A)D... for múltiplo de 7. Isso porque 98 = 100 - 2 é múltiplo de 7, então o que esta operação faz é trocar 100 A por 2 A. Exemplos: 1645 -> 665 -> 65 + 12 -> 77 (múltiplo de 7); 3192 -> 192 + 60 -> 252 -> 56 (múltiplo de 7); 9876 -> 876 + 180 -> 1056 -> 76 (não é múltiplo de 7).
Divisibilidade por 8
editarUm número é divisível por 8 quando os três últimos algarismo forem 0 ou formarem um número múltiplo de 8.
Exemplo:
- 24512 → é divisível.
Divisibilidade por 9
editarUm número é divisível por 9 quando a soma dos valores absolutos de seus algarismos for divisível por 9.
Exemplo:
- 927 (9+2+7=18) → é divisível.
Divisibilidade por 10
editarUm número é divisível por 10 quando termina em zero.
Exemplo:
- 154.870 → é divisível
A divisibilidade por 11
editarSegue uma regra parecida com a da divisibilidade por 7. A título de exemplo considere o número 154.
- Separe o último algarismo
- 15 e 4
- Subtraía o segundo do primeiro, ou seja,
- 15 - 4 = 11.
Como 11 é divisível por 11, então 154 também o é.
Num contra-exemplo, usaremos o número 277. Pelo algoritmo teremos 27 e 7; 27 - 7 = 20, que não é divisível por 11, e portanto 277 também não o é.
O algoritmo pode ser aplicado várias vezes no caso de números maiores.
- Dica: Números que seguem a forma "ABBA" são divisíveis por 11.
- Por exemplo: para 1221, temos A = 1 e B = 2.
Uma regra prática para números grandes é somar os algarismos de posição par e os de posição ímpar. Se as somas forem iguais ou os restos das divisões por 11 forem iguais, então o número é múltiplo de 11. Ou seja, em um número da forma ABCDEFG, compara-se A+C+E+G com B+D+F
- Exemplo: 783178 é divisível por 11, porque 7+3+7 = 8+1+8 = 17. Analogamente, 703175 também é, porque o resto da divisão das duas somas por 11 são iguais, 7+3+7=17 tem resto 6 e 0+1+5=6 também tem resto 6.
Dois exemplos com números grandes:
- 4611686018427387901307445734561825860123058430092136939501844674407370955160 → , portanto é divisível.
- 4611686018427387903307445734561825860223058430092136939511844674407370955161 → , portanto não é divisível.
Divisibilidade por
editarUm número é divisível por quando seus últimos n algarismos forem 0 ou divisíveis por
Divisibilidade por
editarUm número é divisível por quando a soma dos valores absolutos de seus algarismos for divisível por
Números primos
editarNúmero primo é um número natural maior que 1 e que tem exatamente dois divisores positivos distintos: 1 e ele mesmo. Se um número natural é maior que 1 e não é primo, diz-se que ele é um número composto. Por convenção, os números 0 e 1 não são primos nem compostos.
Decomposição em fatores primos (fatoração)
editarO Teorema Fundamental da Aritmética afirma que qualquer número inteiro positivo pode ser escrito como o produto de vários números primos (chamados fatores primos). O processo que recebe como argumento um número composto e devolve os seus fatores primos chama-se decomposição em fatores primos (fatoração).
Exemplos:
Máximo Divisor Comum (MDC)
editarO máximo divisor comum (também conhecido por maior divisor em comum) entre dois números e (vulgarmente abreviada como ) é o maior número inteiro encontrado, que seja divisor dos outros dois. Por exemplo, A definição abrange qualquer número de termos.
Exemplo:
Esta operação é tipicamente utilizada para reduzir equações a outras equivalentes:
Seja o máximo divisor comum entre e e também e o resultado da divisão de ambos por respectivamente.
Então, o seguinte se verifica:
Cálculo
editarPode-se calcular o MDC de duas formas:
- Fatoração conjunta (ou algoritmo de Euclides, ou ainda Processo das divisões sucessivas)
- Fatoração disjunta
Fatoração disjunta
editarFaz-se a fatoração de cada termo separadamente para, depois, multiplicar os fatores comuns de menor expoente.
- Exemplo
24 | 2 12 | 2 6 | 2 3 | 3 1 | 2³ • 3
40 | 2 20 | 2 10 | 2 5 | 5 1 | 2³ • 5
Com efeito,
MDC = 2³ = 8
Fatoração conjunta (algoritmo de Euclides)
editarNa Fatoração conjunta (ou algoritmo de Euclides, ou ainda Processo das divisões sucessivas) fatora-se simultaneamente até dois números.
Monta-se a tabela com a seguinte estrutura:
A | B | R1 | R2 | R... R1 | R2 | R... | 0
onde,
A = um dos números B = o outro número = quociente da divisão = resto da divisão (em seguida, ele torna-se o divisor de B) E assim em diante.
O último resto (antes do 0) será o MDC.
- Exemplo
3 3 80 | 24 | 8 ← MDC (8) 8 | 0
Mínimo Múltiplo Comum (MMC)
editarO Mínimo Múltiplo Comum (também conhecido por menor múltiplo em comum) entre dois números e (vulgarmente abreviada como ) é o menor número inteiro encontrado, que seja múltiplo dos outros dois. Por exemplo,
Cálculo
editarPode-se calcular o MMC de duas formas:
- Fatoração conjunta
- Fatoração disjunta
Fatoração conjunta
editarFaz-se a fatoração com todos os n termos, simultaneamente:
- Exemplo
24, 40 | 2 12, 20 | 2 6, 10 | 2 + 3, 5 | 3 1, 5 | 5 1, 1 | 120
Fatoração disjunta
editarFaz-se a fatoração de cada termo separadamente para, depois, manter-se a base em comum e o expoente maior, multiplicado pelos fatores não comuns.
- Exemplo
24 | 2 12 | 2 6 | 2 x 3 | 3 1 | 2³ • 3
40 | 2 20 | 2 x 10 | 2 5 | 5 1 | 2³ • 5
Com efeito,
23 • 3 • 5 8 • 3 • 5 120,
Propriedades do MDC e do MMC
editarRelação de Bézout:
Algoritmo de Euclides:
MDC(a, b)=MDC(a, b-a)
MDC(a, b)=MDC(a, r), onde r é o resto da divisão de b por a.
Ver também
editarWikilivros
editarExercícios:
Uma abordagem mais avançada:
Wikipédia
editarNúmeros inteiros
editarDefinição
editarOs inteiros, ou números inteiros, consistem dos números naturais (0, 1, 2, ...) e dos números inteiros negativos (-1, -2, -3, ...). O conjunto de todos os inteiros é normalmente chamado de Z (Mais apropriadamente, um Z em blackboard bold, ), que vem de Zahlen (do alemão, "número").
Inteiros podem ser adicionados ou subtraídos, multiplicados e comparados. A principal razão para a existência dos números negativos é que tornou possível resolver todas as equações da forma:a + x = b para a incógnita x; nos números naturais apenas algumas destas equações eram solúveis.
Como os números naturais, os inteiros formam um conjunto infinito contável.
= {...,-3,-2,-1,0,1,2,3,...}
Se retirarmos o desses conjuntos, obtemos o subconjunto:
= {...,-3,-2,-1,1,2,3,...}
Outros subconjuntos de
- Conjunto dos inteiros não-negativos:
= {0,1,2,3,...}
- Conjunto dos inteiros não-positivos:
= {...,-3,-2,-1,0}
- Conjunto dos inteiros positivos:
= {1,2,3,...}
- Conjunto dos inteiros negativos:
= {...,-3,-2,-1}
Notas:
- =
- =
Veja também
editarWikilivros
editar- Álgebra abstrata/Números inteiros - uma abordagem mais avançada
Wikipedia
editarNúmeros racionais
editarNúmeros racionais e frações
editarFração é um número que exprime uma ou mais partes iguais que divida uma unidade ou um inteiro.
Assim, por exemplo, se tivermos uma pizza inteira e a dividirmos em quatro partes iguais, cada parte representará uma fração da pizza.
Na matemática, um número racional (ou, vulgarmente, fração) é uma razão entre dois inteiros, geralmente escrita na forma onde é um número inteiro diferente de Zero.
Exemplos:
A adição e multiplicação de racionais é dada da seguinte forma:
Exemplo:
- + =
Dois números racionais a/b e c/d são iguais apenas se ad = bc.
O conjunto de todos os números racionais é Q, ou:
Cada número racional pode ser escrito de diversas formas, como, por exemplo, 3/6 = 2/4 = 1/2. A forma mais simples é quando a e b não possuem divisores em comum, e todo racional tem uma forma como esta. A expansão decimal de um racional é finita ou periódica, propriedade que caracteriza os números racionais.
Definições
editarDe modo simples, pode-se dizer que uma fração de um número, representada de modo genérico como designa este número dividido em partes iguais. Neste caso, corresponde ao numerador, enquanto corresponde ao denominador.
Por exemplo, a fração designa o quociente de por Ela é igual a pois x =
Nota: A divisão é a operação inversa da multiplicação.
Os números expressos em frações são chamados de números racionais. O conjunto dos racionais é representado por
- = { / = com e }
Decimais
editarDecimais exatos
editar=
=
Decimais periódicos
editar= (a)
= (b)
Os decimais periódicos são denominados dízimas periódicas. As dízimas periódicas podem ser simples como no exemplo (a) ou compostas como no exemplo (b). A fração que originou a dízima periódica é denominada de fração geratriz e a parte que repete na dízima é denominada período.
Geratriz de dízima periódica
editarDízima simples
editarA fração geratriz é obtida usando-se como numerador o período e como denominador um número formado por tantos noves quantos forem os algarismos do período.
Dízima composta
editarA fração geratriz terá como numerador a parte não-periódica, seguida do período menos a parte não-periódica, e denominador um número formado de tantos noves quanto são os algarismos do período, seguido de tantos zeros quantos são os algarismos da parte não-periódica (ante-período).
=> + = + = =
Conversão entre dízima e fração
editarSeja o número x = 2,333... (dízima). O período da dízima é o número 3 (um só dígito), assim, para colocar o período da dízima antes da vírgula, fazemos 10*x = 23,333.... Agora, podemos eliminar a dízima fazendo a subtração: 10*x - x = 23,333... - 2,333..., ou seja, 9*x = 21 x =
Outro exemplo mais complexo desta conversão, que ocorre quando a dízima se apresente mais à frente da vírgula: x = 38,07821821821... (dízima). Após a virgula, temos os números "07"´(dois dígitos) que não fazem parte do período e o período "821" (três dígitos).
Primeiro isolamos o período logo após a vírgula:
100*x = 3807,821821821...
Agora repetimos o processo do exemplo anterior:
100.000*x = 3807821,821821821...
Fazemos então a subtração
100.000*x - 100*x = 3807821,821821821... - 3807,821821821..., assim, temos que
99900*x = 3804014 , portanto
x = , que poderá ainda ser simplificada.
Como decorrência da repetição deste processo de conversão, podemos chegar à seguinte regra prática de conversão de dízimas em frações. Vamos aplicá-la ao número 38,07821821821...
Eis os passos:
1. O período da dízima tem 3 dígitos, que é o número de algarismos nove (999 portanto);
2. Após a vírgula temos 2 dígitos que não fazem parte da dízima, que é o número de zeros (00 portanto);
3. Temos assim o denominador da fração que será 99900;
4. O númerador da fração será a diferença do número formado pelos algarismos até o primeiro período da dízima, no caso 3807821, pelo número formado pelos algarismos que antecedem o início da dízima, no caso 3807. Temos então 3807821 - 3807.
5. A fração será, portanto, .
Tipos de frações
editar- própria: o numerador é menor que o denominador. Ex.:
- imprópria: o numerador é maior que o denominador. Ex.:
- mista: constituída por uma parte inteira e uma fracionária. Ex.:
- aparente: o numerador é múltiplo do denominador. Ex.:
- equivalentes: aquelas que mantêm a mesma proporção de outra fração. Ex.:
- irredutível: o numerador e o denominador são primos entre si, não permitindo simplificação. Ex.:
- unitária: o numerador é igual a 1 e o denominador é um inteiro positivo. Ex.:
- egípcia: fração que é a soma de frações unitárias, distintas entre si. Ex:
- decimal: o denominador é uma potência de 10. Ex.:
- composta: fração cujo numerador e denominador são frações:
- contínua: fração constituída a partir de uma sequência de inteiros naturais da seguinte maneira Quando esta fração contínua termina, o seu resultado é um número racional, porém quando esta fração não termina, o resultado pode ser racional ou irracional.
Operações
editarMultiplicação
editarMultiplicam-se os numeradores entre si e os denominadores entre si. Ex.:
Para multiplicar uma fração por um número inteiro, considera-se que este é uma fração cujo denominador é igual a 1. Ex.:
É importante notar que, muitas vezes, a multiplicação dos numeradores e denominadores resulta em frações redutíveis. Esta fração deve ser reduzida a uma fração irredutível:
Costuma ser mais prático simplificar antes de efetuar a multiplicação:
Divisão
editarComo visto, a divisão é a operação inversa da multiplicação. É importante ter isso em mente para resolver uma divisão entre frações:
- ÷
Primeiramente inverte-se o divisor da segunda fração. Com isto, tem-se a inversão da operação, isto é, passará a haver uma multiplicação:
Que se resolve como mostrado acima.
Adição
editarCaso os denominadores não sejam iguais é preciso, antes de efetuar a adição, encontrar o menor múltiplo comum (MMC) entre os denominadores:
Encontrado o MMC, este será dividido por cada um dos denominadores, multiplicando-se o resultado desta divisão pelo respectivo numerador. Como o MMC de 3 e 5 é 15, tem-se que:
- ∴ ∴
Sendo iguais os denominadores, pode-se efetuar a adição entre os numeradores:
O denominador comum é mantido:
Subtração
editarA subtração é feita seguindo-se os mesmos passos da adição.
Exponenciação
editarÉ indiferente resolver primeiro a exponenciação ou a divisão:
Efetuando-se primeiramente a divisão obtém-se o mesmo resultado:
Radiciação
editarA radiciação de uma fração é feita seguindo-se os mesmos passos da potenciação.
Expoente fracionário
editarDa mesma forma que na divisão entre frações, a ocorrência de expoente fracionário causa a inversão da operação:
Simplificação de frações
editarUma fração pode ser simplificada quando numerador e denominador não são primos entre si. Ex.:
Para tanto basta dividi-los pelo máximo divisor comum (MDC) entre eles, obtendo-se uma fração que, além de manter a proporção da original, é do tipo irredutível:
Comparação entre frações
editarPara estabelecer comparação entre frações, é preciso que elas tenham o mesmo denominador. Isso é obtido através do menor múltiplo comum, como foi visto na adição.
- ?
O MMC entre 5 e 7 é 35.
- ∴ ∴
Uma vez igualados os denomidores,pode-se fazer a comparação entre as frações:
- < ∴ <
A comparação entre frações com denominadores diversos vale-se do fato de que há frações que são equivalentes entre si, pois:
- e
Conversão entre frações impróprias e mistas
editarUma fração do tipo imprópria pode ser convertida para mista e vice-versa.
Para tanto, basta dividir o numerador pelo denominador. O quociente será o numerador da fração mista e o resto será o numerador. Como o quociente da divisão 7 ÷ 3 é igual a 2 e o resto é 1, tem-se que a fração acima, escrita como fração mista, terá a seguinte notação:
Para fazer o caminho inverso, basta multiplicar o denominador pela parte inteira e somar o resultado ao numerador, mantendo-se o denominador. Como o produto 3 × 2 é igual a 6 e a soma 6 + 1 é igual a 7, obtém-se novamente a notação sob a forma de fração imprópria, como visto acima.
Ver também
editarWikilivros
editar- Matemática elementar/Conjuntos/Números racionais/Exercícios
- Análise real/Números racionais - texto mais avançado
Wikipédia
editarNúmeros irracionais
editarO conjunto dos números irracionais é um subconjunto dos números reais. Distingue-se dos números racionais, pois não pode ser representado por , sendo a e b números racionais. Todos os números reais são infinitos e não são periódicos. Portanto, é usual os números irracionais serem representados por símbolos. Veja, abaixo, algumas constantes que são números irracionais utilizadas na matemática:
- π (Pi Radiano) = 3,141592...
- e (Número de Euler) = 2,718281...
- φ (Número de Ouro) = 1,618033...
Raízes irracionais
editarTambém são considerados números irracionais as raízes de números primos:
- √2 = 1,414213...
- √3 = 1,732050...
- √5 = 2,236067...
- 3√2 = 1,259921...
Os múltiplos destas raízes também o são:
- √6 = √2.3 = 2,449489...
- √10 = √2.5 = 3,162277...
- √30 = √2.3.5 = 5,477225...
Os múltiplos de raízes de números primos resultarão em números racionais , se, e somente se em
o quociente entre todos os expoentes (a, b, c, ...) dos números primos (x, y, z, ...) e o índice n forem números inteiros. Exemplo:
O quociente entre os expoentes dos números primos e o índice é: 4÷2 = 2; 2÷2 = 1; -2÷2 = -1. Já que todos são inteiros, a raiz de 5,76 é racional, e equivale a 2,4.
Operações em
editar- Adição - Uma adição x + y, em que ao menos uma das variáveis é irracional, resultará em um número irracional (exceto se x = -y). Exemplo:
- π + 1 = 4,141592...
- π + √2 = 4,555806...
- √2 + √3 = 3,146264...
- Subtração - Em uma subtração x - y, em que ao menos uma das variáveis é irracional, o resultado será um número irracional (exceto se x = y). Exemplo:
- π - 1 = 2,141592...
- √10 - π = 0,020685...
- √7 - √10 = -0,516526...
- Multiplicação - Se em uma multiplicação um dos fatores for irracional, o produto será também irracional (exceto se um dos fatores for zero, ou se ocorrer a repetição de uma mesma raiz n vezes, em que n também é o índice). Exemplo:
- √2 x √3 = √6
- 3√2.3√2.3√2 = 2 (observe que o índice das raízes coincidiu com o número de vezes em que ela repetiu na multiplicação, originando, portanto, um número racional).
Inconsistente o exemplo logo acima, porque multiplicar dois números irracionais, iguais ou distintos entre si, resulta num número irracional.
Não é porque o número irracional está representado por (raiz enésima (a)), ele passa a ser racional. Então, mesmo que eu eleve (raiz enésima (a)) à enésima potência, o resultado não será "a", e sim um número que tende a "a". Se formos pensar sobre essa questão, veremos que, se tivermos b = (raiz enésima (a)), com "b" pertencente ao conjunto dos números irracionais, e "a" e "n" pertencentes ao conjunto dos números racionais, então a extração de (raiz enésima (a)) é impossível.
- Divisão - Uma divisão que envolva um número irracional, resultará em outro número irracional (exceto se o mesmo número irracional multiplique n vezes tanto no denominador quanto no numerador, ou se o número zero estiver presente). Exemplo:
- √6 ÷ √3 = √2
- 2√2 ÷ √2 = 2 (veja que o mesmo número irracional repetiu a mesma quantidade de vezes no divisor e no dividendo).
- Potenciação - Uma potenciação que envolva um número irracional sempre resultará num número irracional (exceto se o expoente for zero, ou o quociente entre o expoente do radicando e o índice for um número inteiro). Exemplo:
- π2 = 9,869604...
- (√3)4 = 9 (pelo fato de a razão entre o expoente do radicando e o índice ser um número inteiro, 4 ÷ 2 = 2, a potenciação não originou um número irracional).
Também é inconsistente o exemplo logo acima, pelo mesmo motivo de que falei em "Multiplicação".
Bem, se os intelectuais que lerem meus comentários duvidarem, então façam assim: extraiam a raiz quadrada de dois, à mão, consoante o Método Exato de Extração de Raízes Quadradas, explanado em Wikipedia, em "Raiz quadrada". Extraiam-na, indo a partir da primeira até, no mínimo, a quintitilionésima casa decimal após a vírgula; depois, elevem cada resultado ao quadrado, também à mão. Se algum dos, no mínimo, cinco milhões, der 2,000000000000000000000000..., eu retifico esse comentário. Caso não der, eu estarei certo.
Não basta só teorizar. Tem que, provar, na prática.
Números reais
editarConceito
editarEm matemática, potências são valores que representam uma multiplicação sucessiva de um número, ou seja, representam o mesmo número multiplicado algumas vezes por si mesmo. Uma potência é composta por um número, chamado base, que é multiplicado sucessivamente por si mesmo; e por um índice, chamado expoente, que diz o número de vezes que a base é multiplicada por si mesma. As potências apresentam-se na forma onde n é o expoente e x é a base.
A potência por exemplo, indica que a base, o número 4, será multiplicada sucessivamente 3 vezes por si mesma, ou seja Se o expoente é 1, então o resultado tem o valor da base (), enquanto que com um expoente 0, devido a regras de operações feitas diretamente com potências, o resultado é sempre igual a 1 ( = 1).
Propriedades da potenciação
editarPrimeira propriedade
editarAo multiplicar potências de mesma base, repetimos a base e somamos os expoentes.
Segunda propriedade
editarAo dividir potências de mesma base, repetimos a base e subtraímos os expoentes.
Terceira propriedade
editarAo elevar uma potência a um outro expoente, repetimos a base e multiplicamos os expoentes.
Quarta propriedade
editarAo elevar um produto ou um quociente a um expoente, elevamos cada um dos fatores a esse expoente ou, no caso do quociente, elevamos o dividendo e também o divisor ao mesmo expoente.
Equivalência entre bases
editarÉ importante perceber que, mesmo com bases diferentes, podemos torná-las iguais para efetuar uma operação. Exemplo:
Podemos substituir 4 por 22:
Expoentes negativos
editarQuando temos um número elevado a n em que n < 0, podemos dizer que:
Observe que a fração foi invertida e o sinal negativo do expoente desapareceu. Exemplo:
Tópicos
- Definição de Potência
- Operações com potências
- Multiplicação
- Com a mesma base
- Com o mesmo expoente
- Com a mesma base e o mesmo expoente
- Divisão
- Com a mesma base
- Com o mesmo expoente
- Com a mesma base e o mesmo expoente
- Multiplicação
- Equações envolvendo potências
- Inequações envolvendo potências
- Gráficos de funções exponenciais
Exercícios
editarVer: Matemática elementar/Exponenciais/Exercícios
Radiciação
editarPropriedades da radiciação
editarRacionalização de denominadores
editarExercícios
editarVer: Matemática elementar/Números reais/Exercícios
Intervalos reais
editarIntuitivamente, um intervalo real é um subconjunto dos números reais que não tem nenhum buraco. Ou seja, se I é um intervalo, a e b são elementos deste intervalo com a < b, então todo número entre a e b também pertence ao intervalo.
Os intervalos são classificados de acordo com seus extremos (o extremo superior e o extremo inferior). Cada extremo pode ser ilimitados, limitado e aberto ou limitado e fechado.
Representa-se o intervalo através do seu limite inferior, seguido da vírgula (ou ponto-e-vírgula) e o limite superior.
Costuma-se representar o limite inferior por:
- - ilimitado
- - limitado e aberto
- - limitado e fechado
Sendo o limite superior representado por:
- - ilimitado
- - limitado e aberto
- - limitado e fechado
Por exemplo:
- - é o conjunto dos números reais não-positivos
- - é o conjuntos dos números reais x em que x ≥ 1 e x < 2
Exercícios
editarVer: Matemática elementar/Números reais/Intervalos reais/Exercícios
Veja também
editar- Análise real/Os números reais - uma abordagem mais avançada
Wikipédia
editarExercícios
editarSobre Radiciação
editar- Coloque em ordem crescente:
- Expresse sob a forma de raiz as expressões abaixo:
- Os lados de um triângulo valem cm, cm e cm. Calcule seu perímetro.
- Simplifique os radicais
- Racionalize as expressões abaixo:
- Transforme as expressões em um único radical:
- Coloque a expressão na forma mais simples, conforme o exemplo do exercício 1:
- = = =
- Escreva as expressões abaixo como uma soma de radicais:
- Seja x um número real positivo tal que é o inverso de . Determine .
- Seja e . Determine a:b.
- Simplifique as expressões abaixo:
== Veja também ==Leonardo Belo Nato
- Matemática elementar/Exponenciais/Exercícios
- Matemática elementar/Números reais/Intervalos reais/Exercícios
Números complexos
editarO conjunto dos números complexos é a extensão dos números reais. Esta extensão é toda construída a partir de um elemento novo, a unidade imaginária . Tipicamente, números deste conjunto são designados por z, mas é permitido utilizar qualquer signo para representá-los.
O número imaginário
editarA unidade imaginária i - que define os números complexos - tem o valor de √-1. Para esta, então, podemos considerar todas as regras de radiciação. Observe o exemplo abaixo:
Desta forma, raízes negativas podem ser facilmente reduzidas a um número complexo. Esta característica é muito utilizada para descobrir raízes de funções em que o discriminante é menor que zero. Por exemplo, as raízes de f(x) = x2 + 9 são dadas por

Soma por um número real
editarA soma de um número imaginário por um número real origina o afixo do número complexo z. Desta forma, em um número complexo z cujo afixo é dado por a + bi, teremos a como a parte real (denotada por Re), e b a parte imaginária (denotada por Im). Desta forma, teremos:
- b igual a zero para um número real qualquer;
- a igual a zero para um número imaginário puro qualquer.
Já para a - bi, teremos o conjugado do número complexo. O conjugado de um número complexo z é dado por z. Por exemplo, o conjugado do número z = 2 - i é
Que resulta em z = 2 + i.
Operações com os complexos
editarSoma e subtração
editarO seguinte fragmento resume a soma e a subtração dos números complexos:
Por exemplo, considere os números complexos z1 e z2, para z1 = -2 + 4i e z2 = -3 - i, então z1 + z2 =
Conclui-se a soma pela obtenção de -5 + 3i.
A subtração pode ser deduzida a partir da adição. Veja a diferença entre z1 e z2:
Que é igual a 1 + 5i.
Multiplicação
editarA própria definição do conjunto dos números complexos reside na multiplicação. Assim, definimos o conjunto dos números complexos como tendo a seguinte operação de multiplicação:
Na prática, isto resume-se na multiplicação distributiva:
Exemplo: z1z2, para z1 = 2 + i e z2 = -1 + 2i:
Potenciação
editarVocê deve ter notado a presença de expoente acima da unidade imaginária no exemplo anterior. A potência pode e deve ser resolvida. Facilmente ela pode ser deduzida. Veja:
Para expoentes maiores que três (x), a seguinte operação é válida:
Em que k é o maior inteiro possível para {y ∈ N| 0 ≤ y ≤ 3}. Por exemplo, i20:
Divisão
editarA divisão de números complexos pode ser feita pelo método da chave. Entretanto, esta última muitas vezes pode ser demorada até que se obtenha resto igual a zero. Geralmente, o método aplicado consiste na multiplicação do denominador e numerador pelo conjugado do divisor. Exemplo:
O conjugado do divisor é igual a -1 - 2i. Portanto:
Representação geométrica
editar- É denominado de norma de um complexo z, dado por , o quadrado da parte real somada ao quadrado da parte imaginária, ou seja, .
- E, denomina-se módulo (ou valor absoluto) de z, ao seguinte real e positivo:
- Veja o módulo que trata sobre o plano de Argand-Gauss.
Veja também
editarUma abordagem mais avançada dos números complexos pode ser vista no livro Análise complexa/Introdução.
Relações
editarRelações são, conforme visto no capítulo anterior, quaisquer subconjuntos do produto cartesiano A × B. Em verdade, as relações podem envolver produtos cartesianos de vários conjuntos (X1 × X2 × ... × Xn), e a relação específica que envolve o produto cartesiano de dois conjuntos é chamada relação binária.
Assim, uma relação binária é o conjunto de pares ordenados cujo primeiro elemento pertence a A e o segundo elemento pertence a B, quaisquer que sejam os conjuntos A e B. Representa-se a relação binária por . O conjunto A é chamado de domínio da relação, o conjunto B é chamado de contradomínio da relação.
Especificando relações
editar
A imagem à direita mostra uma maneira comum de se especificar relações: através de figuras mostrando os dois conjuntos, com setas indicando os pares ordenados.
As relações também podem ser especificadas matematicamente da seguinte maneira:
- ,
Onde C é uma condição qualquer que associe os elementos de A e B. Pode ser uma equação ou inequação. Por exemplo:
- A = { 1,2,3 }
- B = { 1,2,3,4,5,6 }
A relação, cujo domínio é A e o contradomínio é B, é especificada por y = 2x. Logo, R = { (1,2),(2,4),(3,6) }.
- C = { 1,2,4,8 }
- D = { 0,1,2 }
- R = { (1,2) }
Representação gráfica
editar
Relações binárias, visto consistirem de pares ordenados, podem ser representadas em gráficos. Um gráfico é nada mais do que uma curva (o nome se aplica mesmo a gráficos com apenas retas) que representa visualmente a relação binária, para cada par ordenado em que ela se defina. O gráfico formado assim é também chamado de sistema cartesiano ou gráfico cartesiano, por representar um produto cartesiano.
Uma relação que tenha por coordenadas elementos pertencentes ao conjunto dos números reais é representada, usualmente, num plano com duas retas: o eixo das abcissas e o eixo das ordenadas. Estas retas recebem também os símbolos x e y, respectivamente.

No caso da relação ser definida por inequações, o gráfico correspondente vai representar áreas, e não curvas. (Por razões práticas, no gráfico muitas vezes aparece colorida ou hachurada apenas uma parte, logo abaixo ou acima de uma linha que define a inequação.)
Um gráfico pode estar "em branco" para relações definidas pelo conjunto vazio ({}).
No gráfico como apresentado o eixo das abcissas representa o domínio da relação, e o eixo das ordenadas representa o contra-domínio da relação.
Função
editarExiste um tipo especial de relação que é chamado função: é a relação na qual, para todo elemento do domínio, há correspondência de um (e somente um) elemento no contradomínio. A função normalmente é simbolizada por f(x) (sendo x uma variável, ou seja, um valor que pode representar qualquer elemento do conjunto domínio).
Como conseqüência natural da correspondência biunívoca entre elementos do domínio e contradomínio, a função é sempre uma relação definida por uma equação (pois uma inequação associa um elemento do domínio a vários elementos do contradomínio).
As funções são estudadas com mais detalhes no próximo capítulo.
Relações de equivalência
editarUma classe muito importante de relações são as de equivalência, que serão definidas a seguir. Seja R uma relação entre os conjuntos A e B, ou seja, R ⊆ A×B. Denotaremos que um elemento a de A se relaciona com o elemento b de B, segundo a relação R, por aRb. Se uma relação R definida com domínio A e contradomínio A cumpre as seguintes propriedades: ∀a A aRa (propriedade reflexiva) ∀a,b A aRb ⇔ bRa (propriedade simétrica) ∀a,b,c A aRb e bRc ⇒ aRc (propriedade transitiva) Ela é dita Relação de Equivalência.
Relações de equivalência permitem que se definam classes de equivalência. Seja ā = {x A | xRa}. ā é denominado classe de equivalência de a. Alguns resultados importantes desta definição são:
Teorema: Se a ē ⇒ ā=ē Demonstração: Tome x ā. Por definição xRa. Como a ē, por definição aRe. Pela propriedade transitiva das relações de equivalência, xRe, logo x ē. Tome x ē. Por definição xRe. Como a ē, por definição aRe, logo, eRa. Pela propriedade transitiva das relações de equivalência, xRa, logo x ā. Deste modo, ā=ē.
Teorema: Se a∉ē, então ā∩ē=∅ Demonstração: Suponha, por absurdo que existe um x em ā∩ē. Da definição de interseção de conjuntos e da definição de classes de equivalência, xRa e xRe. Logo aRx e xRe. Daí aRe. Deste modo, a ē. Isto é um absurdo pela hipótese. Deste modo, nenhum x pode pertencer a ā∩ē. Logo ā∩ē=∅.
Teorema: Se ā≠ē, então ā∩ē=∅ Demonstração: Se ā≠ē, então existe u ā tal que u∉ē ou u ē tal que u∉ā. Suporemos, sem perda de generalidade, que existe u ā tal que u∉ē. Como já provamos ū=ā e ū∩ē=∅. Logo ā∩ē=∅.
Definição: Uma partição de um conjunto X é um conjunto P tal que x P ⇒ x⊆X, além de x,y P ⇒ x∩y=∅ e x X ⇒ ∃a P tal que x a.
Teorema: Seja R uma relação de equivalência em A, P={ā⊆A|a A} é uma partição de A. Demonstração: Mostramos, no teorema anterior, que os elementos de P são subconjuntos de A, o que cumpre a primeira condição da definição de partição. Dois elementos de P, se são distintos, são disjuntos, conforme provamos no teorema anterior. E, para todo u em A, ū pertence a P, pela definição de P. Deste modo P é uma partição de A.
Teorema: Seja P uma partição de A, a relação R dada por aRe ⇔ a ē é de equivalência. Demonstração: a ā por definição, de modo que aRa para todo a em A. Se aRe, então a ē, logo ā=ē. Daí, como e ē por definição, então e ā. Logo eRa Se aRe e eRu, então a ē e e ū. Daí, sabemos que ā=ē=ū. Logo a ū e, portanto, aRu. Deste modo, provamos as três condições da definição de relação de equivalência.
Disto sabemos que toda partição induz uma relação de equivalência e toda relação de equivalência induz uma partição. Estes resultados são muito úteis em vários ramos da Matemática, como Geometria.
Funções
editarUma função é uma relação especial, que é definida da seguinte maneira: sejam dois conjuntos A e B, tais que para todo elemento x pertencente a A, haja uma correspondência de um elemento y pertencente a B. Essa correspondência é a função: a associação, definida de algum modo, entre todos os elementos de um conjunto e os elementos de outro conjunto.
A função que associa um elemento x a outro valor pode ser indicada por f(x). O aparecimento de x na simbologia da função não ocorre por acaso, uma vez que o valor f(x) depende de x. Por isso mesmo, x é chamada variável independente e f(x) (ou y) é chamada de variável dependente. Matematicamente a função é definida:
- , ou mais simplificadamente,
Um exemplo de função: dado o conjunto dos números naturais, uma função pode associar cada número ao seu quadrado. Assim, essa função assumiria os valores: { 1,4,9,16,... }.
Uma função pode, na verdade, associar mais de um conjunto a outro; pode haver diversas variáveis independentes. Por exemplo: uma função pode tomar dois valores inteiros e expressar sua soma:
No entanto, neste livro será dada mais atenção às funções de uma variável, apenas. São duas características da função enquanto relação:
- há correspondência unívoca entre um elemento e o valor associado a ele pela função: isso significa que para cada valor assumido pela variável independente (x), há um único valor da variável dependente (y) associado pela função. Consequentemente, se t = f(x) e w = f(x), então t = w.
- a correspondência é total, ou seja, um valor assumido pela variável dependente estará associado para todo valor possível de ser assumido pela variável independente.
A tabela a seguir mostra dois exemplos de relações que não são funções:

|

|
| Nesse caso, um mesmo elemento (3) do domínio X aparece associado a dois elementos do contradomínio Y (c,d). | Aqui a correspondência não é total: falta um valor associado a 1. |
Já o diagrama a seguir representa uma função:
Duas funções f e g são ditas iguais (f = g) se e somente se para cada valor de x no domínio D, f(x) e g(x) assumam o mesmo valor:
- OBS.: uma função é uma relação, por isso não possui grau. Quem possui grau são os polinômios associados a função. Dessa maneira é um equívoco pensar em "função de 1° ou 2° graus".
Introdução
editarRelações que estabeleçam dependência entre os elementos de dois conjuntos são denominadas funções.
Um exemplo clássico de função é a do salário de vendedores que ganham por comissão:
Existe um valor fixo que o vendedor ganha mesmo se não conseguir vender nada naquele mês e uma comissão, que depende da quantidade de vendas que o vendedor realizou. Por exemplo:

| Vendas | Comissão por venda | Valor Fixo | Salário |
| 0 | 55 | 300 | 300 |
| 1 | 55 | 300 | 355 |
| 2 | 55 | 300 | 410 |
| ... | ... | ... | ... |
Da tabela acima podemos construir uma relação entre as vendas e o salário do vendedor:
E com isso, construímos um gráfico que relaciona vendas a salário, onde verifica-se que:
- O salário depende das vendas.
- O salário é uma função das vendas.
Definição
editarAo aplicar uma função em um dado conjunto , cada elemento deste deverá ter como correspondente um elemento em um dado conjunto .
Ao conjunto denomina-se domínio da função, sendo seus elementos denominados abscissas, e ao conjunto denomina-se contra-domínio, sendo seus elementos denominados ordenadas ou imagens, quando estas se correlacionarem a um elemento de .
Ou seja:
Dados dois conjuntos e não vazios, dizemos que a relação f de em será função se, e somente se,
- .
(Para qualquer x pertencente a D existe um y pertencente a C tal que o par ordenado (x,y) pertence à função f)
- Obs: Para cada , deve haver apenas um
Representações
editarExistem várias maneiras de se representar funções.
Abaixo você pode ver as três mais comumente utilizadas, sendo a primeira a predominante.
As representações abaixo são de uma função em relação a seu domínio e contra-domínio.
Há também as representações por sua fórmula algébrica em relação a sua imagem, como a seguir:
Condições de existência
editarAs condições básicas de existência são:
- Todo e qualquer elemento do domínio deve possuir uma única imagem no contra-Domínio.
- Caso a equação algébrica da função contenha uma fração, seu denominador deve ser diferente a 0 (zero).
- Caso a equação algébrica da função possua uma raíz de índice par, para que seu resultado pertença aos Reais, o radicando deve ser maior ou igual a 0 (zero).
- Caso essa mesma raíz esteja no denominador de uma fração, o radicando deve ser estritamente maior que 0 (zero).
- Caso o índice dessa raíz seja um número ímpar, a única restrição é que o radicando seja diferente de 0 (zero).
Com isso, cada função deverá ter suas restrições particulares, mas sempre obedecendo as gerais acima. Algumas regras não são aplicáveis a funções com contradomínio Complexo.
Nomenclaturas
editarAbaixo você confere o que significa cada nome utilizado ao se falar sobre funções:
Domínio, contradomínio e imagem
editar
São três conjuntos especiais associados à função. O domínio é o conjunto A do exemplo dado no início deste capítulo: contém todos os elementos x para os quais a função deve ser definida. Já o conjunto B do exemplo é o contradomínio: o conjunto que contém os elementos que podem ser relacionados a elementos do domínio.
Também define-se o conjunto imagem como o conjunto de valores que efetivamente f(x) assume. O conjunto imagem é, pois, sempre um subconjunto do contradomínio.
Por exemplo, suponha a função que associa um elemento do domínio D = { 1,2,3,4,5 } a uma vogal ordenada no alfabeto.
- O domínio, já especificado, é
- O contradomínio é
- A imagem é
Gráfico Cartesiano
editar- Abscissa
- Todo e qualquer elemento do domínio.
- Ordenada
- Todo e qualquer elemento do conjunto imagem.
- Gráfico em Plano Cartesiano da função
- Representação de todos os pontos que compõem uma função através de dois eixos perpendiculares.
Funções Sobrejetoras, Injetoras e Bijetoras
editarFunções Pares e Ímpares
editar- Uma função é denominada par quando , para todo (domínio de f).
- Uma função é denominada ímpar quando , para todo .
Propriedades das funções
editarContinuidade
editarUma função é dita contínua sobre um intervalo dado, , se possui um valor definido para todos os números contidos nesse intervalo. Por exemplo, a função:
- , definida para o contradomínio , não é contínua no intervalo , uma vez que não está definida para x < 0.
Crescimento e decrescimento
editarUma função é dita crescente, sobre um intervalo [A,B], se para cada valor de x + ε (ε sendo qualquer valor positivo), .
Uma função é dita decrescente, sobre um intervalo [A,B], se para cada valor de x + ε (ε sendo qualquer valor positivo), .
Paridade
editarA paridade de uma função é uma propriedade relacionada a simetria da mesma, e portanto só pode ser definida para funções cujo domínio é simétrico (veja a definição de conjunto simétrico). Sendo um elemento pertencente a um conjunto simétrico , uma função é dita:
- par, se para todo , ; ou seja, o valor da função é definido apenas de acordo com o módulo da variável independente;
- ímpar, se para todo , ;
- sem paridade, se não corresponder a nenhum dos dois casos anteriores.
Funções polinomiais de primeiro e segundo graus
editarExistem dois tipos especiais de funções a respeito das quais cabe fazer comentários aqui. Uma função é dita polinomial do primeiro grau ou afim quando pode ser expressa na forma:

A função polinomial do primeiro grau sempre toma no gráfico a forma de pontos colineares. Se o domínio da função for o conjunto R, tem-se uma reta.
O valor da constante , na função e que tem domínio igual a , é chamado coeficiente angular da reta que define a função. Ele pode ser obtido a partir da relação entre quaisquer dois pontos da reta (ou valores associados da variável independente e dependente), conforme a equação:
Para o caso específico da constante ser igual a zero, a função é chamada função linear.

.
Já a função do segundo grau toma a forma:
Graficamente, a função do segundo grau é sempre uma parábola, cuja concavidade depende unicamente do sinal da constante a. Se a for negativo, a parábola tem o vértice voltado "para cima"; se a for positivo, a parábola tem o vértice voltado "para baixo". (Considerando a representação usual do plano cartesiano.)
Operações sobre funções
editarSoma, produto e quociente
editarComposição de funções
editarO conceito de uma função é uma generalização da noção comum de "fórmula matemática". Funções descrevem relações matemáticas entre dois objetos, e . O objeto é chamado o argumento da função , e o objeto , que depende de , é chamado imagem de pela .
Intuitivamente, uma função é uma maneira de associar a cada valor do argumento um único valor da função . Isto pode ser feito especificando através de uma fórmula ou regra de associação, um gráfico, ou uma simples tabela de correspondência...
Alguns tipos de funções
editarPropriedades fundamentais, gráficos, máximos, mínimos, equações e inequações envolvendo estas funções.
- Função polinomial
- Função exponencial e Função logaritmica
- Função trigonométrica
- Função modular
- Função afim
Funções sobrejetoras, injetoras e bijetoras
editarTomemos dois conjuntos e . Digamos que o primeiro seja um conjunto de crianças e o segundo é de mulheres adultas. Seja f a função que leva cada criança x do conjunto X na sua mãe y = f(x) do conjunto Y.
- Se houver ao menos uma criança no conjunto que não seja filha de uma mulher do conjunto , então esta relação não consiste em uma função.
- Se houver ao menos uma criança no conjunto que seja filha de mais de uma mulher do conjunto , então esta relação também não consiste em uma função.
- Se no conjunto X não houver nenhum par de irmãos, ou seja, as mulheres do conjunto Y tem apenas um filho ou nenhum filho, então temos que para a e b crianças diferentes do conjunto X, as suas mães f(a) e f(b) são diferentes. Neste caso, a função é injetora.
- Se o conjunto Y for formado apenas de mães, ou seja, não há mulheres sem filho em Y, então qualquer que seja a mãe m do conjunto Y existe alguma criança c tal que f(c) = m (ou seja, m é a mãe de c). Neste caso, a função é sobrejetora.
- Se não houver irmãos em X, e o conjunto Y for formado de mães, então existe uma correspondência perfeita entre crianças e suas mães, ou seja, toda criança tem só uma mãe e toda mulher tem só um filho. A função f é, ao mesmo tempo, injetora e sobrejetora, ou seja, é bijetora.
-
Função Injetora e não sobrejetora
-
Função Sobrejetora e não injetora
-
Função Bijetora
- Resumindo:
- Função Injetora (ou função injetiva, ou uma injeção) é aquela na qual dois elementos diferentes no domínio correspondem sempre a elementos diferentes no contra-domínio.
- Função sobrejetora (ou função sobrejetiva ou uma sobrejeção) é aquela na qual o contra-domínio é igual à imagem, ou seja, cada elemento do contradomínio é correspondido por ao menos um do domínio.
- Função bijetora (ou função bijetiva ou uma bijeção) é aquela na qual para cada elemento no domínio corresponde a um único elemento no contradomínio, e cada elemento no contradomínio corresponde a um único do domínio.
No restante do texto, serão estudadas funções numéricas, ou seja, funções entre conjuntos de números reais.
Domínio finito
editarQuando o domínio da função é finito, a forma mais prática de verificar se a função é injetora, sobrejetora ou bijetora é calcular diretamente f(x) para cada ponto do domínio, e verificar:
- se existem x e y diferentes com f(x) = f(y), então a função não é injetora
- se existe algum y no contra-domínio que ficou de fora, ou seja, para o qual não existe x com f(x) = y, então a função não é sobrejetora
Exemplo
editarSeja A = { -2, -1, 0, 1, 2}, B = {0, 1, 2, 3, 4}, C = {0, 1, 4}, D = {0, 1, 2} e as funções:
- dada por k(x) = 1
- dada por g(x) = x2
- dada por h(x) = x2
- dada por f(x) = x + 2
Então:
- e não é injetora, porque e(0) = e(1). e também não é sobrejetora, porque não existe x tal que e(x) = 0.
- f não é sobrejetora, porque não existe x tal que f(x) = 2. Mas f é injetora: a única forma de f(x) ser igual a f(y) é quando x = y, como pode ser visto listando os pares ordenados de f: {(0, 0), (1, 1), (2, 4)}.
- g não é injetora, porque g(-1) = g(1). Mas g é sobrejetora, porque para todo elemento y de C existe um elemento (pode haver mais de um) x de A com g(x) = y. Isto pode ser visto também listando os pares de g: {(-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4)}. Outra forma de ver que ela é sobrejetora é observar que a imagem de g é o conjunto {0, 1, 4}, igual ao contra-domínio C.
- h é injetora, porque se h(x) = h(y), então x + 2 = y + 2 logo x = y. h também é sobrejetora, porque para todo elemento y de B existe um x de A com h(x) = y. De fato, isto pode ser visto enumerando-se os pares de h, ou observando-se que a imagem de h é o conjunto B.
Casos particulares
editarAlguns casos particulares para funções , em que A e B são conjuntos finitos de números
- Se f é injetora, então A não tem mais elementos que B
- Se f é sobrejetora, então A não tem menos elementos que B
- Se f é bijetora, então A tem tantos elementos quanto B
- Se f é uma função do primeiro grau, f(x) = a x + b, com a ≠ 0, então f é injetora.
Deve-se notar que estas regras não são suficientes para resolver todos os casos, por exemplo a função dada por f(x) = x2, em que A = {-1, 1} e B = {0, 1} não é nem injetora nem sobrejetora.
Domínio e contra-domínio real
editarNeste caso temos uma função .
Alguns casos particulares:
- Se f é uma função do primeiro grau, f(x) = a x + b, com a ≠ 0 então f é bijetora.
- Se f é uma função do segundo grau, f(x) = a x2 + b x + c, com a ≠ 0, então f não é injetora nem sobrejetora.
Em outros casos, deve-se procurar desenhar o gráfico da função.
Exemplo
editar Considere a função dada por f(x) = (x - 1)(x - 2)(x - 3).
Considere a função dada por f(x) = (x - 1)(x - 2)(x - 3).
Obviamente, pelo gráfico é fácil ver que esta função não é injetiva. Pela equação também é fácil, já que f(1) = f(2) = f(3) = 0.
Esta função é sobrejetiva. Este fato e sugerido pelo gráfico, apesar deste mostrar apenas parte do conjunto imagem.
Domínio e contra-domínio intervalos de números reais
editarNeste caso temos uma função , em que A e B podem ser toda a reta real, intervalos finitos ou intervalos infinitos.
A única regra especial é:
- Se f é uma função do primeiro grau, f(x) = a x + b, com a ≠ 0 então f é injetora.
Ver também
editarArtigos na wikipedia:
Função inversa
editarDada uma função , uma pergunta natural é, dado um valor v do contradomínio, em que condições a equação f(x) = v tem uma solução única x = u ?
Por exemplo, para funções do primeiro grau, de domínio e contra-domínios reais, f(x) = a x + b (em que a ≠ 0), a equação f(x) = v admite a única solução .
Por outro lado, para funções reais do segundo grau f(x) = a x2 + b x + c (novamente, a ≠ 0), a equação f(x) = v pode possuir duas, uma ou nenhuma raiz (dependendo do valor de ser, respectivamente, positivo, zero ou negativo).
Como outro exemplo, a função f(x) = x2 + 1, quando o domínio é o conjunto dos números reais positivos e o contra-domínio é o conjunto dos números reais maiores que um é tal que f(x) = v sempre admite uma única solução. Isto porque, sendo v > 1, temos que x2 + 1 = v é equivalente a x2 = v - 1, ou seja, a solução é a (única) raiz quadrada positiva do número positivo v - 1 dada por .
Conceito
editarDada uma função , dizemos que é a função inversa de f quando:
- Para todo valor , a equação f(x) = y tem uma solução
- Esta solução é única, e dada por x = g(y).
Teoremas
editar- Se a função f tem uma inversa, então f é uma função bijetora.
- Se f é uma função bijetora, então f tem uma inversa, e a função inversa é bijetora
- A função inversa de uma função é única
- Se g é a função inversa de f, então f é a função inversa de g
Definições relacionadas
editar
Uma função que tenha inversa diz-se invertível.
A função inversa de uma função f é representada por f-1 - note-se que esta notação deve ser usada com cuidado, pois, em alguns contextos, .
Ver também
editarArtigo na wikipedia:
Exponenciais
editarDefinição de Potência
editarEm matemática, potências são valores que representam uma multiplicação sucessiva de um número, ou seja, representam o mesmo número multiplicado algumas vezes por si mesmo. Uma potência é composta por um número, chamado base, que é multiplicado sucessivamente por si mesmo; e por um índice, chamado expoente, que diz o número de vezes que a base é multiplicada por si mesmo. As potências apresentam-se na forma , onde n é o expoente e x é a base.
A potência , por exemplo, indica que a base, o número 4, será multiplicada sucessivamente 3 vezes por si mesma, ou seja . Se o expoente é 1, então o resultado tem o valor da base (), enquanto que com um expoente 0, devido a regras de operações feitas diretamente com potências, o resultado é sempre igual a 1 ( = 1).
A regra para o expoente zero pode parecer estranha. Mas se não fosse assim, todas as propriedades de potências ficariam mais complicadas. Além disto, quem olhar um gráfico de uma função exponencial vai ver que não poderia ser de outra forma. Enfim, tudo induz para que aceitemos esta forma de definir as potências com expoente 0.
Operações com Potências
editarExistem várias regras que visam facilitar a resolução de potências. É possível multiplicar e dividir qualquer par de potências que possuam a mesma base, o mesmo expoente, ou os dois iguais.
Multiplicação
editarCom a mesma base
editar| Para efetuar a multiplicação de potências com as bases iguais e expoentes diferentes, mantém-se a base e somam-se os expoentes. |
Com o mesmo expoente
editar| Para multiplicar duas potências com os expoentes iguais e bases diferentes, mantém-se o expoente e multiplicam-se as bases. |
Com a mesma base e o mesmo expoente
editar|
|
Para multiplicar duas potências com os expoentes iguais e as bases também iguais, pode-se utilizar qualquer uma das regras. |
Divisão
editarCom a mesma base
editar| Para dividir duas potências com as bases iguais e expoentes diferentes, mantém-se a base e subtraem-se os expoentes. |
Com o mesmo expoente
editar| Para dividir duas potências com os expoentes iguais e bases diferentes, mantém-se o expoente e dividem-se as bases. |
Com a mesma base e o mesmo expoente
editar
|
Para dividir duas potências com os expoentes iguais e as bases também iguais, pode-se utilizar qualquer uma das regras. |
(1) - Este caso nos dá mais um motivo para tomarmos qualquer potência com expoente 0 como sendo igual a 1. Como e então .
Observe que isto não é a prova que pois foi utilizada uma propriedade para subtrair os expoentes, propriedade esta que, para ser provada, necessita que seja considerado , logo, não pode ser provada utilizando a equação acima.
Equações envolvendo potências
editarEquações do tipo af(x) = bg(x)
editarEquações do tipo
onde a é uma constante são resolvidas simplesmente igualando-se f(x) a g(x).
No caso mais geral:
é preciso, primeiro, converter uma (ou ambas) bases para que as duas bases fiquem iguais.
Exemplo
editar- Resolva:
O primeiro passo é transformar as bases. No caso, pode-se transformar ou (exercício), mas é bem mais simples transformar e :
Aplicando a propriedade :
Agora temos uma equação da forma :
Verificando:
- (ok)
Equações do tipo f(ax) = 0
editarAs equações do tipo
são resolvidas de forma análoga à biquadrada. Lembrando: uma biquadrada é resolvida pela substituição . Resolve-se a equação em y, e, com o(s) valor(es) de y, resolve-se a equação em x.
Exemplo
editar- Resolva a equação
De novo, como temos bases diferentes, é conveniente reescrever tudo para a mesma base. Como , temos:
Usando agora a propriedade :
Ainda temos um problema! É preciso transformar em uma expressão onde esteja isolado. Para isto, vamos usar a propriedade :
Então a expressão fica:
Resolvendo:
Aplicando a fórmula de Bhaskara:
Ou seja, as duas raízes são:
A primeira solução, y = -3, gera uma equação sem solução em x, porque é sempre um valor positivo e não pode ser igual a -3.
A segunda solução fornece:
Ou seja:
- x = -1
Verificando, temos que:
- (ok)
Inequações envolvendo potências
editarGráficos de funções exponenciais
editarExercícios
editar- Ver Exercícios
81²+81²+81²=
Ver também
editar|
Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros. |
Exercícios
editarA seguir são sugeridos alguns exercícios sobre exponenciais.
- Simplifique as expressões abaixo, conforme o exercício 1:
- Simplifique as expressões abaixo:
- Simplifique as expressões abaixo:
- Sendo a = 43, b = (-8)5, c = (-2)6 e d = (1/2)-3, determine o valor de:
- Escreva Verdadeiro (V) ou Falso (F), corrigindo a resposta no segundo caso:
- ( )
- ( )
- ( )
- ( )
- Se n é um número par, ( )
- Se n é um número ímpar, ( )
- ( )
- ( )
- ( )
- Se a é diferente de zero, ( )
- ( )
- ( )
- ( )
- ( )
- ( )
- ( )
- ( )
- ( )
- ( )
- Simplifique as expressões:
- Sendo x > 0 e y > 0,
Logaritmos
editar
Considere o seguinte exemplo:
Uma família decidiu construir sua árvore genealógica. Enquanto desenhavam-na, notaram que a cada geração superior, dobrava o número de ascendentes. Na última geração, havia um. Na penúltima, dois. Na antepenúltima, quatro, e assim sucessivamente.
Qual a geração em que há 128 pessoas? É simples:
No entanto, há a impossibilidade de resolver o cálculo. Para isto, algumas calculadoras possuem a tecla log2:
Portanto, a geração em que há 128 ascendentes é a sétima geração anterior à primeira.
A tecla log nada mais faz que descobrir um logaritmo.
Definição de logaritmo
editarUm logaritmo pode ser descrito como:
Observe que em cada operação (logaritmo, potência e raiz) um elemento diferente está em evidência. Isto mostra qual destes (a, b ou c) é necessário para a resolução da equação. Sendo apenas a inversão de outras duas operações, as propriedades dos logaritmos são idênticas às das potências e raizes.
Vejamos um exemplo numérico abaixo:
Neste caso, dizemos que 2 é a base e 8 é o logaritmando. Assim, 3 é o logaritmo de 8 na base 2.
Observação: quando o valor da base não está explicita, considera-se 10 para a base:
Equações envolvendo logaritmos
editarExistem basicamente três métodos para a resolução de equações com logaritmos:
Desenvolvimento na forma de potência
editarNa resolução de equações envolvendo logaritmos é de grande ajuda em certas situações usar princípios de equações exponenciais. Nestes casos, convertemos o logaritmo para uma potência. Por exemplo:
Que pode ser entendida como:
Esse tipo de comparação facilita a compreensão do problema em questão e de muitos outros semelhantes. Neste caso, basta pensarmos a que expoente devemos elevar a base 3 para obtermos a potência 27. Conclui-se que x = 3, pois 33 = 27.
Logaritmo como variável
editarO logaritmo pode também ser entendido como uma função. Por exemplo, se temos uma função x, operamos com os princípios da álgebra, e isto ocorre também com os logaritmos. Exemplo:
Na álgebra, para podermos operar termos é necessário que a parte literal de cada monômio seja igual. Com os logaritmos isto ocorre de forma similiar:
Para podermos operar logaritmos de forma análoga à álgebra, é fundamental que a base e o logaritmando sejam iguais. Veja outro exemplo:
Com logaritmos podemos interpretar de maneira semelhante:
Logaritmo em funções compostas
editarAlém de aparecer em parcelas de uma soma ou em fatores, como visto nos dois últimos exemplos, o logaritmo pode aparecer em qualquer outra função! Pode estar no quociente de uma divisão, no expoente de uma potência, no radicando de uma raíz, ou até mesmo no logaritmando de um outro logaritmo. Em alguns casos, é muito comum recorrermos a alguma substituição para podermos visualizar melhor a equação. Por exemplo:
| Exemplo de substituição em função composta |
|---|
:
|
Função logaritmica
editarNa tabela abaixo, vejamos os resultados obtidos na função f (x) = log2 x:
| f (x) | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x |

Note que os resultados obtidos seguem um progressão geométrica, e portanto, o gráfico será representado por uma curva. Pode-se observar, ainda, nesse exemplo, que quanto menor for f (x), mais próximo de zero será x, mas não há valor para x que faça y ser nulo. Neste caso, o intervalo do domínio da função é (0, +∞).
Chamamos de raíz da função os valores de x em que f(x) = 0. Isto é, os pontos em que a curva intersepta o eixo das abscissas. No exemplo anterior, isto ocorre quando x = 1.
Vejamos o caso abaixo, de f(x) = (-2)x
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| f(x) |
Veja que os valores de f (x) possuem alternância de sinal, o que faz haver descontinuidade. Desta forma, uma função do tipo loga b = c em que a < 0 não apresentaria um gráfico, e portanto, não existe. Esta é uma regra: a base não pode ser negativa!
Consequentemente, o logaritmando jamais será negativo, pois potências negativas existem somente se a base é negativa e o expoente é ímpar.
Estudo de casos
editarVejamos alguns casos que envolvam logaritmos (desenvolveremos na forma de potência) :
- Temos que logx x = y é o mesmo que xy = x. Pensemos, qual expoente que elevado a uma base qualquer produz uma potência igual a base? O único expoente que satisfaz esta condição é 1, portanto logx x = 1.
- Sabemos que logx 1/x = y é igual a xy = 1/x. O único expoente que elevado a uma base qualquer que produz uma potência inversa a base é -1. Logo, logx 1/x = -1.
- Já que logx 1 = y é o mesmo que xy = 1, devemos pensar quais expoentes deixam qualquer base real positiva igual a 1. O único expoente é o zero, assim, logx 1 = 0.
Operações com logaritmos
editarExistem várias regras que visam facilitar a resolução de logaritmos. Para as demonstrações a seguir, consideraremos logca = x, e logcb = y. Assim, cx = a, e cy = b.
Soma
editarDemonstração:
- Podemos utilizar a propriedade do produto de potências:
- Convertemos o último resultado de potência para logaritmo:
- Como cx = a, cy = b, logca = x e logcb = y, substiuímos termos correspondentes:
Multiplicação por constante
editarDemonstração:
- A partir de:
- Transformamos o último resultado em logaritmo:
- Substituindo os termos correspondentes:
Subtração
editarDemostração:
- Podemos transformar a expressão na seguinte forma:
- Assim, temos uma soma de logaritmos, sendo que um deles está multiplicado por uma constante (-1). Aplicaremos, então, a propriedade do produto por uma constante:
- Utilizado a propriedade do expoente negativo, teremos:
- Considerando a propriedade da soma de logaritmos:
- Portanto:
Mudança de base
editar- Consideraremos os valores para a demonstração:
- (I)
- (II)
Demonstração:
- Para chegar ao resultado da expressão, tomamos o seguinte valor inicial:
- Multiplicaremos as duas últimas equações por x/y:
- Aplicaremos a propriedade da multiplicação por constante na primeira equação:
- Usaremos a propriedade da potência de uma potência (multiplicação de expoentes):
- Substituímos com o resultado em (II):
- Sabemos cx em (I):
- Substituimos x pela primeira equação de (I) e y pela primeira equação de (II):
Que prova a igualdade da propriedade.
| Exemplo de aplicação |
|---|
| Além de frequentemente ser utilizada para simplificar cálculos, a mudança de base permite que calculemos qualquer logaritmo na calculadora. Normalmente, as calculadoras estão providas somente de log10. Consideremos o exemplo localizado no inicio da página:
Se não for possíver realizar o cálculo com a base 2, utilizemos a propriedade da mudança de base: |
Outras propriedades
editarAs quatro propriedades descritas anteriormente (soma, subtração, multiplicação e mudança de base) são fundamentais para o cálculo de logaritmos. Existem outras propriedades que podem ser deduzidas através das operações, que auxiliam em problemas que envolvem logaritmos. São elas:
Inversão do logaritmando
editarEsta propriedade foi utilizada anteriormente na demonstração da substração de logaritmos de mesma base. Pela propriedade, temos que:
Demonstração:
- Multiplicando A = log (x/y) por -1, teremos:
- Utilizando a propriedade da multiplicação por constante:
- Que resulta em
Bases com expoentes
editarDemonstração:
- Pela propriedade da mudança de base, temos que:
- Podemos retirar c do logaritmando pela propriedade da multiplicação por constante:
- Temos um caso de logaritmos em que a base é igual ao logaritmando (logb b), que é igual a 1:
- (I)
- Reescrevendo:
- Pela multiplicação por constante:
- Observe que em (I), podemos ter um final diferente para esta propriedade, ao multiplicarmos a equação por c:
| Exemplo de aplicação |
|---|
| Esta propriedade pode ser aplicada para facilitar a soma ou subtração de logaritmos de bases diferentes. Exemplo:
A propriedade da soma não pode ser utilizada pois as bases dos logaritmos são diferentes. Então colocaremos um expoente na base de modo que estas, posteriormente, fiquem iguais: Aplicando a propriedade da base com expoente: E por fim, poderemos utilizar a propriedade da soma para descobrir y: Simplificando com a multiplicação por constante: |
Troca da base pelo logaritmando
editarDemonstração:
- Pela propriedade da mudança de base, temos que:
- Ocorreu o caso de um logaritmo no qual a base é igual ao logaritmando (logxx), que é igual a 1:
- Elevando-se a equação a -1, podemos reescrevê-la
Divisão e multiplicação de logaritmos
editarPodemos simplificar uma divisão de logaritmos através da propriedade da mudança de base, na qual é necessário que os logaritmos tenham a mesma base:
Demonstração:
- A multiplicação também é definida pela mudança de base. Na equação abaixo, desmembramos o denominador da divisão:
- Dividindo a equação por logca:
- Elevando-se a equação a -1:
- Utilizando a propriedade da troca da base pelo logaritmando:
- Multiplicando a equação por logca:
Que prova a multiplicação de logaritmos.
Cologaritmos
editarCologaritmos são definidos pela seguinte expressão:
Pela propriedade da inversão do logaritmando, podemos reescrevê-los como:
Exercícios
editarTrigonometria
editarTrigonometria
editar
Trigonometria (do grego trigonon = três ângulos e metro = medida) é uma parte da Matemática que estuda as relações entre triângulos, ângulos e funções circulares como o seno e cosseno.
- Trigonometria do triângulo retângulo
 Arcos e ângulos - medida de um arco (radianos), relação entre arcos e ângulos.
Arcos e ângulos - medida de um arco (radianos), relação entre arcos e ângulos. Razões trigonométricas na circunferência
Razões trigonométricas na circunferência Funções trigonométricas
Funções trigonométricas Fórmulas de Adição, subtração, duplicação e bissecção de arcos
Fórmulas de Adição, subtração, duplicação e bissecção de arcos Transformações de soma de funções trigonométricas em produtos
Transformações de soma de funções trigonométricas em produtos Identidades trigonométricas básicas
Identidades trigonométricas básicas Equações e inequações envolvendo funções trigonométricas
Equações e inequações envolvendo funções trigonométricas Lei dos senos e dos cossenos
Lei dos senos e dos cossenos Resolução de triângulos
Resolução de triângulos
Ver também
editarArcos e ângulos
editarCircunferência
editarSeja um ponto qualquer do plano e um número real. A circunferência de centro e raio é o lugar geométrico dos pontos desse plano tais que

Veja no Wikicionário círculo.
Arco de circunferência
editarConsideremos uma circunferência de centro Sejam e dois pontos distintos de

Um arco de circunferência de extremos e é cada uma das partes em que fica dividida uma circunferência por dois de seus pontos.
Quando teremos dois arcos: o arco nulo (um ponto) e o arco de uma volta (uma circunferência).

Arco de circunferência e ângulo central correspondente
editar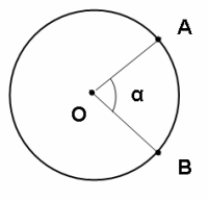
A medida de um arco é, por definição, a medida do ângulo central correspondente. Medir significa comparar com uma unidade padrão previamente adotada. Contudo, para evitar possíveis divergências na escolha da unidade para medir um mesmo arco, as unidades de medida restringem-se a três principais: o grau (), o radiano () e o grado, sendo este último não muito comum.
O grau
editar
Um grau é um arco de circunferência cujo comprimento equivale a da circunferência que contém o arco a ser medido. Portanto, a medida, em graus, de um arco de uma volta completa (uma circunferência) é
- Submúltiplos do grau
- O minuto ou seja,
- O segundo ou seja, e
O radiano
editarUm radiano é um arco de circunferência cujo comprimento é igual ao raio da circunferência que contém o arco a ser medido. É a unidade do Sistema Internacional (SI).
Conseqüentemente, para medir um ângulo em radianos, convém calcular a razão entre o comprimento do arco pelo raio ou seja, calcular quantos radianos mede o arco Portanto, como consequência da definição de radiano, podemos estabelecer a seguinte relação:
onde e devem estar na mesma unidade de comprimento.
O comprimento de uma circunferência de raio é Logo, a medida do arco de uma volta completa, em radianos, é Para converter unidades, podemos usar as correspondências ou e uma regra de três simples.
O grado
editarVer artigo na wikipedia Grado O grado foi introduzido junto com o Sistema métrico, durante a Revolução francesa mas, ao contrário do sucesso das outras medidas, não pegou. Atualmente, ele é apenas utilizado nos trabalhos topográficos e geodésicos feitos na França.
É a medida de um arco cujo comprimento equivale a da circunferência que contém o arco a ser medido. É evidente que, para conversão de unidades, pode-se utilizar as relações ou e uma regra de três simples.
O ciclo trigonométrico
editarConsideremos no plano um sistema de eixos perpendiculares em que Seja uma circunferência de centro raio e o ponto

A cada número real associaremos um único ponto de
- Se então tomamos
- Se realizamos, a partir de um percurso de comprimento no sentido anti-horário e marcamos o ponto como final desse percurso.

- Se realizamos, a partir de um percurso de comprimento no sentido horário, e marcamos o ponto como final desse percurso.

Assim, a circunferência sobre a qual foi fixado o ponto como orientação é chamada ciclo trigonométrico ou circunferência trigonométrica.
O ponto é chamado imagem de no ciclo trigonométrico.
O sistema de eixos perpendiculares divide o ciclo trigonométrico em quatro partes, cada uma das quais é chamada quadrante.

Ângulos côngruos
editarOs ângulos e em graus, são côngruos ou congruentes se, e somente se, para algum ou seja, se e têm a mesma imagem no ciclo trigonométrico. Para indicar que e são côngruos escrevemos
Por exemplo, os ângulos e são congruentes, pois
Expressão geral dos arcos que têm imagem em um ponto do ciclo trigonométrico..
editarConsideremos um sistema de eixos perpendiculares e uma circunferência de centro e raio Sendo um ponto qualquer pertencente à a imagem de um ângulo na circunferência, podemos estabelecer uma expressão geral dos arcos que têm imagem em um determinado ponto do ciclo trigonométrico.

Por exemplo, a expressão geral dos arcos que têm imagem no ponto dar-se-á por ou sendo o número de voltas completas. Quando deve-se andar no sentido anti-horário; se deve-se andar no sentido horário.
Analogamente, temos:
- Para ou
- Para ou
- Para ou
- Para ou ou
- Para ou ou
- Para ou ou ou ou

Considerando a figura acima, a expressão geral dos arcos que têm imagem em ou é:
- em graus:
- em radianos:
Expressão geral dos arcos que têm imagem em
- em graus:
- em radianos:
No caso da figura seguinte, a expressão geral dos arcos fica:

- em graus:
- em radianos:
Primeira determinação positiva
editarA primeira determinação positiva de um ângulo é o menor ângulo côngruo que seja positivo.
Por exemplo, os ângulos (em graus) -15o, 315o, 2115o, -2505o são congruentes, sendo sua primeira determinação positiva o ângulo 315o.
Analogamente, os ângulos (em radianos) , e são congruentes, sendo sua primeira determinação positiva o ângulo .
Para se resolver o problema de determinar a primeira determinação positiva é preciso:
- dividir o ângulo pelo valor do círculo trigonométrico (360o ou , conforme o problema seja apresentado em graus ou radianos)
- se este número não for inteiro, arredondar o valor para o valor inteiro imediatamente inferior
- tomar o número inteiro com sinal contrário (ou seja, se o passo anterior obteve n, obter agora -n)
- somar ao ângulo inicial este valor inteiro do passo acima multiplicado pelo círculo trigonométrico (360o ou , conforme o problema seja apresentado em graus ou radianos)
Exemplos:
- Se o ângulo inicial é -580o
- Dividir -580 por 360 -> -1,(alguma coisa) (note que não é preciso fazer a divisão até o fim, já que estamos apenas interessados na parte inteira da divisão)
- Não sendo inteiro, tomar a parte inteira -> -2
- Trocar o sinal -> 2
- Somar -580o com 2 x 360o -> 140o
- Se o ângulo inicial é
- Dividir por -> 4
- Sendo inteiro, manter -> 4
- Trocar o sinal -> -4
- Somar com -> 0
- Se o ângulo inicial é
- Dividir por -> ou, aproximadamente, 4,(alguma coisa)
- Não sendo inteiro, tomar a parte inteira -> 4
- Trocar o sinal -> -4
- Somar com ->
Imagens de alguns arcos importantes
editar- Primeira volta no sentido anti-horário:
Ângulos correspondentes
editar- Em graus:
- Em radianos:
Exercícios
editarRazões trigonométricas na circunferência
editar
| Este módulo encontra-se em processo de tradução. A sua ajuda é bem vinda. |
Definição geométrica de seno e cosseno
editarNo círculo unitário mostrado abaixo, um raio unitário foi traçado da origem ao ponto (x,y) sobre o círculo.

A linha perpendicular ao eixo-x que passa pelo ponto (x,y) intercepta o eixo-x no ponto com abscissa x. Analogamente, a linha perpendicular ao eixo-y intercepta este eixo no ponto de ordenada y. O ângulo entre o eixo-x e o raio é α.
A funções trigonométricas de qualquer ângulo α são definidas por:
pode ser definido a partir do seno e cosseno.
Estas três funções trigonométricas pode ser usadas para ângulos medidos em graus, radianos ou qualquer outra medida angular, desde que fique claro qual é a unidade usada.
Funções trigonométricas
editarDefinições
editarFunções trigonométricas são funções angulares, importantes no estudo dos triângulos e na modelagem de fenômenos periódicos. Podem ser definidas como razões de dois lados de um triângulo retângulo, contendo o ângulo ou, de forma mais geral, como razões de coordenadas de pontos no círculo unitário ou, de forma ainda mais geral, como séries infinitas ou como soluções para certas equações diferenciais.
Existem seis funções trigonométricas básicas, cada uma com a sua abreviatura notacional padrão.
- seno ( em português; a maioria das linguagens de programação escrevem ).
- coseno ().
- tangente ().
As últimas quatro funções são definidas nos termos das primeiras duas. Por outras palavras, as quatro equações em baixo são definições e não identidades demonstradas.
- tangente
- secante
- cosecante
- cotangente
O seno, o cosseno e a tangente são as mais importantes.
As inversas destas funções são geralmente designadas de arco-função, isto é, arcsin, arccos, etc., ou adicionando o expoente -1 ao nome, como em sen-1, cos-1, etc. O resultado da função inversa é o ângulo que corresponde ao parâmetro da função. Por exemplo, arcsen(1) = 90°.
Trigonometria do triângulo retângulo
editar
As funções trigonométricas são oriundas das razões dos lados dos triângulos. Com base no triângulo retângulo ao lado, o segmento é a hipotenusa (lado oposto ao ângulo de 90°), o segmento é o cateto adjacente (ao lado) do ângulo α e é o cateto oposto ao ângulo α:
|
|
|
|
|
|
|
|
|
Tais funções são constantes para um mesmo ângulo α, pois dois triângulos formados pelos mesmos ângulos mantêm suas proporções.
As funções trigonométricas são utilizadas em geometria, portanto, para determinar um lado ou um ângulo de um triângulo.
Seno, cosseno e tangente dos ângulos
editarNa tabela abaixo, temos o seno, cosseno e tangente dos principais ângulos em decimais:
| 0° | 5° | 10° | 15° | 20° | 25° | 30° | 35° | 40° | 45° | 50° | 55° | 60° | 65° | 70° | 75° | 80° | 85° | 90° | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Seno | 0 | 0,08 | 0,17 | 0,25 | 0,34 | 0,42 | 0,5 | 0,57 | 0,64 | 0,7 | 0,76 | 0,81 | 0,86 | 0,9 | 0,93 | 0,96 | 0,98 | 0,99 | 1 |
| Cosseno | 1 | 0,99 | 0,98 | 0,96 | 0,93 | 0,9 | 0,86 | 0,81 | 0,76 | 0,7 | 0,64 | 0,57 | 0,5 | 0,42 | 0,34 | 0,25 | 0,17 | 0,08 | 0 |
| Tangente | 0 | 0,08 | 0,17 | 0,26 | 0,36 | 0,46 | 0,57 | 0,7 | 0,83 | 1 | 1,19 | 1,42 | 1,73 | 2,14 | 2,74 | 3,73 | 5,67 | 11,43 | - |
Veja que os valores crescentes de sen x são os mesmos para cos x, entretanto são decrescentes. Além disso, a maioria dos senos, cossenos e tangentes dos ângulos são números irracionais. São, portanto, com infinitas casas decimais não periódicas. Todavia, pode-se obter o valor exato das funções trigonométricas em uma forma algébrica. Você pode conferir a forma algébrica de alguns ângulos clicando aqui (em inglês)
Ângulos notáveis
editar
Os ângulos notáveis (0°, 30°, 45°, 60° e 90°) são ângulos que se pode facilmente obter a forma algébrica por meio de triângulos retângulos. Consideremos um triângulo retângulo que corresponde à metade de um triângulo equilátero de lado 1 uc. Tem, portanto, sua hipotenusa c igual a 1, seu lado a igual a 0,5 uc e seu lado b igual a altura do triângulo equilátero, 0,5 √3 uc. Assim:
Que é o seno de 30° e o cosseno de 60°. O seno de 60° e o cosseno de 30° são obtidos de forma similar:
E assim é possível obter as demais funções trigonométricas para 30° e 60°. Para 45°, considera-se um triângulo retângulo igual à metade de um quadrado de lado 1 uc. Tem, então, hipotenusa de medida √2 uc - a diagonal do quadrado - e os catetos de medida 1 uc - os lados do quadrado:
De forma mais simples, os valores do seno dos cinco ângulos notáveis são o quociente entre x e 2, em que x é a raiz de cada um dos cinco termos a1, a2, a3, a4 e a5 de uma progressão aritmética em que a1 = 0 e a razão é igual a +1. O cosseno destes ângulos é a ordem decrescente da progressão:
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| PA | |||||
| Seno = | |||||
| Cosseno = |
A tangente é obtida pela dividindo-se o seno do respectivo ângulo pelo seu cosseno, pois:
Que resulta:
|
|
|
|
|
|
A tangente de 90° não é definida, pois é impossível que o ângulo entre a hipotenusa e os catetos seja 90°.
Círculo trigonométrico
editarConsiderando um círculo de 1 uc de raio, este tem sua circunferência igual a 2π uc. Portanto, um setor de um grau deste círculo corresponde a:
Podemos transformar a unidade de medida uc (unidades de comprimento) em rad (radianos). Assim, podemos dizer que:
Colocando os ângulos notáveis neste círculo obtêm-se os valores (x; y) em que x é o cosseno do ângulo e y o seno:

Observa-se em tais valores que à medida em que os ângulos avançam de quadrante os valores de seno e cosseno tem seu sinal alternado. É perfeitamente notável que tais funções seguem, então, uma periodicidade infinita, e seus valores repetiram a cada volta do círculo. Deste mesmo círculo, pode-se obter as demais funções trigonométricas, que não são mais que relações do triângulo retângulo entre a origem, a coordenada e ponto (x; 0):

Gráficos
editarPodemos colocar as funções trigonométricas em um plano cartesiano, em que o eixo das abcissas equivale ao ângulo em radianos e o eixo das ordenadas ao contradomínio da função.
Seno
editarColocando-se os resultados obtidos para a função seno num plano, obteremos:

Observe que a função seno é uma função ímpar, pois sen (-x) = -sen x, qualquer que seja x pertencente aos números reais. Note que esta função é composta por infinitos intervalos 2π. Dizemos, então, que o período da função sen (x) é 2π. Quanto ao contradomínio, ele pertence ao intervalo [-1; 1]. A distância entre o centro e o limite da função é a amplitude. Neste caso, a amplitude da função é igual a 1. O gráfico da função seno forma uma senoide. Pode-se determinar o seno de qualquer ângulo através das seguintes equações:
|
|
Para as quais: |
Onde y é um ângulo qualquer e z um número inteiro.
Os únicos números z e w que satisfaçam 500 - 90 (4z + w) = x onde x pertence ao intervalo ]0; 90] é z = 1 e w = 1. Veja:
Cosseno
editarO gráfico da função cosseno é o seguinte:

Esta é uma função par, pois cos (-x) = cos x, qualquer que seja x pertencente ao conjunto dos números reais. Igual à função seno, a função cosseno tem período igual a 2π e amplitude igual a 1. O gráfico da função cosseno forma uma cossenoide. De forma similar à função seno, podemos transformar qualquer ângulo real para 0° < x ≤ 90° e assim obter seu cosseno:
|
|
Para as quais: |
Onde y é um ângulo qualquer e z um número inteiro.
Para que o ângulo y tenha seu cosseno igual ao seno de 30°, w deve ser igual a 3:
Já que a equivalência é verdadeira, há infinitos números z que a satisfazem. No entanto, a questão especifica que este deve ser o maior negativo, portanto, z = -1:
Tangente
editarJá para o gráfico da função tangente, temos:

A função tangente é uma função ímpar pois é o quociente de uma função ímpar e uma função par. É, pois, tan (-x) = - tan x {x ∈ R}. O período desta função é igual a π, e sua amplitude estende-se ao infinito. O gráfico da função tangente forma uma tangentoide. Para determinar a tangente de um ângulo qualquer, temos, para 0° ≤ x < 90°:
Onde y é um ângulo qualquer e z um número inteiro.
O primeiro passo é determinar a qual conjunto pertence -200°. Veja que este encaixa-se perfeitamente em 180z + 90 ≤ y < 180 (z + 1) quando z = -2:
Então,
E assim:
Características
editar
Dados a + b sen (cx - dπ) ou a + b cos (cx - dπ), que são as equações da senoide e da cossenoide, respectivamente, determina-se:
- a + b e a - b - os limites (0; a+b) e (0; a-b) da função trigonométrica, equivalente ao conjunto imagem Im = [a+b; a-b];
- 2π ÷ c - o período da função;
- d - o deslocamento horizontal da função trigonométrica.
A partir destes valores tem-se a amplitude (A), dada pela média aritmética da distância entre as ordenadas dos limites:
Propriedades
editarCosseno ao quadrado mais seno ao quadrado
editar
Diretamente da figura que define seno e cosseno (ao lado), temos, pelo triângulo retângulo no primeiro quadrante, que:
É convencional escrever o quadrado de uma função trigonométrica colocando-se o sinal imediatamente ao lado do nome da função. Assim, esta relação é escrita:
A geometria do triângulo retângulo prova esta relação no caso de ou seja, para ângulos no primeiro quadrante. Nos casos temos que um deles (seno ou cosseno) vale 1, e o outro vale 0, logo a soma dos seus quadrados é 1.
Nos demais casos, temos:
- Se x está no segundo quadrante, então está no primeiro quadrante, e:
- : portanto:
Analogamente:
- Se x está no terceiro quadrante, então está no primeiro quadrante, e:
- : portanto:
Finalmente:
- Se x está no quarto quadrante, então está no primeiro quadrante, e:
- : portanto:
Ou seja, a relação
é válida para qualquer ângulo real x.
Propriedades do quadrado da secante e da cossecante
editarLembrando que:
temos que:
- Dividindo por
- Dividindo por
Exercícios
editarAdição, subtração, duplicação e bissecção de arcos
editarNesta página aprenderemos a efetuar operações trigonométricas que envolvam a adição, subtração ou multiplicação de números reais.
Adição de arcos
editarCosseno da soma
editar
Considere a figura ao lado. Sejam três pontos e pertencentes à circunferência , cujas coordenadas são e Os arcos e têm medidas iguais, logo as cordas e também têm a mesma medida. Após aplicarmos a fórmula da distância entre dois pontos da Geometria analítica, temos:
Ao igualarmos as duas expressões, temos a fórmula:
Seno da soma
editarSabemos que A partir disto e sendo obtemos:
Utilizando a fórmula do cosseno da diferença de dois arcos nessa última expressão:
Substituindo e nesta expressão, então:
Tangente da soma
editarSabendo que e utilizando as fórmulas anteriores para soma de senos e cossenos, podemos facilmente conseguir uma expressão para
Então:
Vale lembrar que essa fórmula só pode ser usada se e porque a relação só é válida se e somente se
Cotangente da soma
editarComo podemos obter, de maneira semelhante à formula da tangente da soma, uma expressão para
Simplificando, temos:
Como é válida se e somente se a identidade que demonstramos acima só pode ser usada se e
Exemplos
editar- Calcule:
- Resolução
Subtração de arcos
editarCosseno da diferença
editarPara calcular fazemos uso da igualdade na fórmula do cosseno da soma, conforme a seguir:
Então:
Seno da diferença
editarPodemos fazer a mesma substituição da igualdade para encontrar as outras relações de diferença de arcos. Para o seno, usaremos a fórmula do seno da soma e a igualdade citada acima, conforme a seguir:
Logo,
Tangente da diferença
editarUsando novamente a igualdade e, desta vez, a fórmula da tangente da soma:
Simplificando, temos:
Pelos motivos já citados anteriormente, esta fórmula só é válida se e
Cotangente da diferença
editarMais uma vez, usaremos a igualdade e, desta vez, a fórmula da cotangente da soma:
Logo, obtemos a identidade:
Está fórmula só pode ser aplicada se e
Exemplos
editar- Calcule:
- Resolução
- Dados e calcule
- Resolução
Multiplicação de arcos
editarÉ possível deduzir fórmulas para calcular as funções trigonométricas de utilizando as fórmulas obtidas para a soma de arcos e fazendo conforme será mostrado adiante.
Cosseno
editarUsando a fórmula do cosseno da soma, temos:
Logo, utilizando a Identidade relacional básica, podemos obter duas fórmulas finais:
ou
Utilizando a Identidade relacional básica e trabalhando algebricamente, temos:
Expressões para são obtidas por processos semelhantes.
Seno
editarUltilizando a fórmula do seno da soma:
Então, temos:
Utilizando a Identidade relacional básica:
Logo:
Expressões para são obtidas por processos semelhantes.
Tangente
editarA partir da fórmula da tangente da soma:
Logo:
Ao subtituimos a fórmula anterior para e simplificarmos, obtemos como fórmula final:
Expressões para são obtidas por processos semelhantes.
Exemplo
editar- Se e calcule
- Resolução
Precisamos encontrar para aplicarmos a fórmula. Para tanto, utilizaremos a identidade que relaciona as funções cotangente e cossecante. A partir da cossecante obtida, podemos encontrar o valor do seno, uma vez que Como o valor da cossecante é positivo.
De onde vem
Podemos finalmente calcular:
Bissecção de arcos
editarCosseno
editarVamos utilizar as duas fórmulas que encontramos para a fim de que, dado o cosseno de uma arco qualquer, possamos obter ou Para isto, consideraremos
A partir de
A partir de temos:
Finalmente, sabendo que temos:
Seno
editarCaso nos seja dado o sabendo que calculamos e usamos as fórmulas dadas logo acima para o cosseno.
Tangente
editarPrecisamos agora encontrar fórmulas que permitam calcular e conhecida a Para tanto, tomaremos as fórmulas de multiplicação
e consideraremos de modo que:
Exemplos
editar- Se com calcule as funções circulares de
- Resolução
Logo, temos:
- Se determine
- Resolução
Podemos aplicar diretamente a fórmula, de modo que:
Exercícios
editar
Esta página foi eleita pelos colaboradores como uma das melhores do Wikilivros. Para mais informações, consulte a página de votações.
Transformações de soma de funções trigonométricas em produtos
editarAs fórmulas de transformação de soma e diferença em produto, também conhecidas como Fórmulas de Prostaférese[1], são:
Dedução - soma e diferença dos senos
editarPartindo das fórmulas do seno da soma de arcos:
Somando-as membro a membro:
Fazendo:
Temos:
Substituindo a e b, em (I):
Procedendo da mesma forma, novamente a partir de:
Subtraindo-as membro a membro:
- (II)
Substituindo a e b, em (II):
Dedução - soma e diferença dos cossenos
editarAgora para a função cosseno
Somando-as membro a membro:
- (III)
Substituindo a e b, em (III):
E por fim:
Subtraindo-as membro a membro:
- (IV)
Substituindo a e b, em (IV):
Exercícios
editarReferências
Identidades trigonométricas básicas
editarConceito
editarUma identidade trigonométrica é uma equação envolvendo funções trigonométricas e que é verdadeira para todos os valores das variáveis envolvidas. Estas identidades são úteis sempre que expressões envolvendo funções trigonométricas tem que ser simplificadas. Geralmente é possível aproveitar as características cíclicas das funções para modificar o seu comportamento, transformando uma ou mais funções trigonométricas em outras operadas de forma que apresentem o mesmo resultado da função original.
Identidade relacional básica
editarUma vez que no ciclo trigonométrico com ângulo podemos encontrar as coordenadas fazendo e podemos verificar que estas coordenadas e a distância entre a origem e o ponto formam um triângulo retângulo. Sendo esta distância unitária, temos:
Portanto:
Equações e inequações envolvendo funções trigonométricas
editarConceito
editarEquações trigonométricas são equações nas quais a variável a ser determinada aparece após a aplicação de funções trigonométricas.
Uma das grandes diferenças entre equações trigonométricas e as demais equações é a natureza periódica destas funções.
Assim, enquanto equações do tipo:
possuem uma solução única, ou uma quantidade finita (e pequena) de soluções, uma equação do tipo:
admite infinitas soluções - por ser tan uma função periódica de período para cada solução x = a, temos que e também serão soluções, assim como qualquer valor sendo k um número inteiro (positivo, negativo ou zero).
Equações do tipo sen(x) = n, cos(x) = n e tan(x) = n
editarsen(x) = n
editarA equação só tem soluções quando está no intervalo [-1; 1]. Se está neste intervalo, então é preciso primeiro determinar um ângulo tal que:
Neste caso, as soluções são dois conjuntos infinitos (que devem ser unidos):
Em que é qualquer inteiro.
Quando n = 1, 0 ou -1, estas soluções tem uma forma mais simples, que podem ser vistas na tabela ao lado.
Exemplo
editarResolva:
Primeiro, deve-se determinar um valor para
Substituindo nas fórmulas, temos:
- ou
Resolvendo estas equações em x chega-se à resposta final:
- ou
Em que k é um número inteiro.
Outro exemplo
editarResolva:
Substituindo
Sabemos que é um ângulo cujo seno vale 1/2. Portanto, y deve valer:
- ou
Substituindo o valor de
- ou
Ou seja:
- ou
Esta solução está correta, mas, normalmente, deseja-se expressar os ângulos na forma em que
Para isso, como k é um número inteiro qualquer, ele pode ser substituído por qualquer outra expressão que também indica um número inteiro qualquer. Ou seja, podemos substituir k por k + 10, k + 42, k - 1000, etc.
No caso, como queremos tornar a parte sem k em um número entre 0 e 2 π, temos que substituir k por k+1, obtendo:
- ou
Finalmente:
- ou
Equações com restrição no domínio
editarDeterminação do domínio
editarEquações com mais de uma função trigonométrica
editarExercícios
editarLei dos senos e dos cossenos
editarLei dos cossenos
editarEm qualquer triângulo, o quadrado de um dos lados é igual à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo formado entre eles. A saber:
Demonstração
editarEsta é uma das maneiras de demonstrar a lei dos cossenos.
Considerando a figura, podemos observar três triângulos:

Destes, pode-se extrair as seguintes relações: e
Usando o Teorema de Pitágoras para obter uma relação entre os lados dos triângulos, temos:
- Para
- Para
Substituindo e em
Entretanto, pode-se substituir a relação do triângulo na equação acima. Dessa maneira, encontra-se uma expressão geral da Lei dos cossenos:
Da mesma forma, pode-se demonstrar as demais relações:
Aplicação
editarA Lei dos Cossenos permite calcular o comprimento de um lado de qualquer triângulo conhecendo o comprimento dos demais lados e a medida do ângulo oposto a esse. Ela também permite calcular todos os ângulos de um triângulo, desde que se saiba o comprimento de todos os lados.
Exemplos
editar- Considere um triângulo de lados e sendo que o comprimento de é 2 metros e o comprimento de é metros. Os lados e definem um ângulo de 30º. Calcule o comprimento de
- Resolução
- Dada a Lei dos Cossenos, tem-se que e portanto:
- O comprimento de é 1 metro.
- Prove por Lei dos Cossenos que o triângulo eqüilátero também é eqüiângulo
- Resolução
- Dado um triângulo eqüilátero de lados e por definição tem-se que Sejam e os ângulos deste triângulo. Aplicando a Lei dos Cossenos:
- O mesmo vale para e
Lei dos senos
editarO seno de um ângulo de um triângulo qualquer é proporcional à medida do lado oposto a esse ângulo. A saber:
Demonstração
editar
Para demonstrar a lei dos senos, tomamos um triângulo qualquer inscrito em uma circunferência de raio A partir do ponto pode-se encontrar um ponto diametralmente oposto e, ligando a formamos um novo triângulo retângulo em
Da figura, podemos perceber também que porque determinam na circunferência uma mesma corda Desta forma, podemos relacionar:
Fazendo todo este mesmo processo para os ângulos e teremos as relações:
e em que é a medida do lado oposto a é a medida do lado oposto a e é uma constante.
Logo, podemos concluir que:
Lei das tangentes
editar
Seja um triângulo não isósceles e não retângulo cujos ângulos internos e medidas dos lados estão indicadas na figura. A lei das tangentes estabelece que, para qualquer triângulo que não seja isósceles nem retângulo, valem as seguintes relações:
Demonstração
editarPara demonstrar a Lei das tangentes, podemos partir da Lei dos senos:
Usando uma propriedade das proporções, temos que:
Substituindo nessa equação as fórmulas de transformação de soma em produto, temos:
Analogamente, pode-se provar as outras duas relações.
Exercícios
editarResolução de triângulos
editarUma das aplicações mais comuns da trigonometria é a resolução de triângulos.
A resolução de triângulos é a operação matemática que, a partir de três elementos de um triângulo, determina todos outros elementos. Estes elementos podem ser lados, ângulos, perímetro, área, etc.
Os casos mais comuns são representados por uma tríade de letras, usando-se L (para lado) e A para ângulo. Assim, LLL significa resolver um triângulo no qual são dados três lados, LAA significa resolver um triângulo no qual é dado um lado, um ângulo adjacente e um ângulo oposto. Nem todos casos são solúveis: AAA pode ter nenhuma (se a soma dos ângulos não for de 180o) ou infinitas soluções; LLA pode ter nenhuma, uma ou duas soluções.
LLL
editarUsa-se a lei dos cossenos para se determinar dois ângulos; o terceiro ângulo sai naturalmente da soma dos ângulos ser 180o.
LAL
editarUsa-se a lei dos cossenos para se determinar o lado oposto ao ângulo. Um outro ângulo pode ser determinado pela lei dos senos ou dos cossenos.
ALA
editarDetermina-se o terceiro ângulo pelos dois ângulos. Os outros lados saem pela lei dos senos.
LAA
editarDetermina-se o terceiro ângulo pelos dois ângulos. Os outros lados saem pela lei dos senos.
LLA
editarDois métodos podem ser usados, mas ambos podem não ter solução:
- Resolve-se o terceiro lado pela lei dos cossenos - neste caso, a equação é uma equação do segundo grau, que pode ter nenhuma, uma ou duas raízes.
- Resolve-se o outro ângulo (que não é o ângulo formado pelos lados) pela lei dos senos - neste caso, a equação também pode ter nenhuma, uma ou duas soluções.
Progressões
editar|
Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros. |
Sequências ou progressões são funções do tipo , onde A é o conjunto dos números naturais ou um subconjunto dos números naturais consecutivos com mais de dois elementos, e B é um conjunto numérico. Sendo funções, nas sequências existe uma regra geral que permite determinar cada elemento de B a partir do elemento A, por exemplo:
- (2,4,6,8,10) é uma sequência dos números pares de 2 até 10, que pode ser expressa pela função . Também percebe-se que a função pode relacionar o elemento anterior (an) com o posterior (an+1) da seguinte maneira: , sendo r uma razão fixa, a razão de progressão.
Os dois tipos de sequências matemáticas mais comuns são a progressão aritmética, que contém números tais que o anterior somado a uma razão fixa resulta no posterior, e progressões geométricas, que contém números tais que o anterior multiplicado pela razão fixa resulta no posterior.
Exemplos:
- (1,5,9,13,...) é uma progressão aritmética infinita (o que se indica pela reticiências ...) de razão igual a 4;
- (1,3,9,27,81) é uma progressão geométrica finita de razão igual a 3.
Sequências numéricas
editar- Matemática elementar/Sequências numéricas
- Matemática elementar/Progressões aritméticas
- Matemática elementar/Progressões geométricas
- noção de limite de uma sequência
Exercícios resolvidos
editar1) Ache tres números em P.A crescente,sabendo que a soma é 15 e o produto é 105.
O problema pode ser resolvido assim: Chame de x o primeiro dos 3 números na PA e de r a razão da mesma. Então os termos são os seguintes: x, x+r, x+2r Como a soma deve ser igual a 15, os números x e r precisam satisfazer a equação: x + x+r + x+2r = 15 ou seja, 3x + 3r = 15 que se reescreve como x + r = 5
Logo, r = 5-x.
Por outro lado, se o produto de tais números é 105, deve ocorrer: x*(x+r)*(x+2r)=105 ou seja, x*(x+5-x)*(x+2(5-x))=105 que pode ser reescrito como 50x-5x^2=105
As raízes dessa equação do segundo grau são 3 e 7 e se obtem rapidamente pela fórmula de Bhaskara.
temos que considerar cada um dos casos: x=3 nessa situação, como r=5-x=5-3=2, os termos da PA são 3, 5 e 7
x=7 deduz-se que r=5-7=-2, donde os termos são 7, 5 e 3
Apenas o primeiro caso representa uma PA crescente, logo a resposta é 3, 5 e 7
2) O perímetro de um triangulo retangulo mede 24 cm.Calcule as medidas dos lados sabendo que eles estão em P.A.
Sabendo que os lados estão em PA, podemos chamá-los de x, x+r e x+2r, e supor que esta é uma PA crescente, como no problema anterior. Mas se o perímetro é 24, ou seja a soma dos lados tem esse valor, então: 3x+3r=24
ou seja x+r=8
donde r=8-x
Mas em todo triângulo retângulo vale o Teorema de Pitágoras, e a hipotenusa é sempre o maior lado, então: (x+2r)^2=(x+r)^2+(x)^2
ou seja, (16-x)^2=8^2+x^2
ou ainda, 256 - 32x + x^2= 64 + x^2
que é equivalente a 32x=256-64=192
Portanto, x=6 e consequentemente r=8-6=2. Assim a resposta deve ser 6, 8 e 10.
Expressões algébricas
editarProdutos notáveis são expressões matemáticas padronizadas, em que um produto ou uma potência pode ser expressa através de uma soma de monômios.
A operação inversa se chama fatoração algébrica, que consiste em expressar um polinômio como o produto de polinômios (usualmente binômios) mais simples.
O desenvolvimento dos produtos notáveis é um passo fundamental na simplificação de expressões que envolvem somas ou subtrações, como na resolução de vários tipos de equação.
A fatoração, por outro lado, é fundamental na simplificação de expressões que envolvem a divisão de polinômios, e também é importante na resolução de equações polinomiais.
Produtos notáveis
editarQuadrado da soma de dois termos
editar.
Exemplos:
Quadrado da diferença de dois termos
editar
Exemplos:
Cubo da soma de dois termos
editar
Exemplos:
Cubo da diferença de dois termos
editar
Exemplos:
Exercícios
editarFatoração algébrica
editarFatoração pelo fator comum em evidência
editarConsidere o polinômio , seu fator comum em evidência é , dividindo cada termo do polinômio pelo fator comum em evidência e , a forma fatorada de um polinômio pelo fator comum em evidência é igual ao produto do fator comum em evidência pelo polinômio obtido da divisão de cada termo do polinômio, logo a forma fatorada de . O fator comum em evidência pode ser aplicado em todos os termos do polinômio.
Outros exemplos:
Fatoração por agrupamento
editarObserve o polinômio . Este polinômio não possui um fator comum para ser aplicado em todo o mesmo, a solução é fazer pequenos grupos de polinômios a partir do polinômio principal, veja:
, logo podemos fatorar os pequenos grupos formados do polinômio principal:
, obtemos a fatoração de , nota-se que os termos entre parênteses são iguais, permitindo uma nova aplicação do fator comum em evidência: . A forma fatorada de .
Outro exemplo:
Fatoração da diferença de dois quadrados
editar
Considere o polinômio , que é uma diferença de dois quadrados, para fatorar o mesmo devemos obter a raiz quadrada do primeiro termo menos a raiz quadrada do segundo termo , logo temos , devemos, agora, multiplicar o polinômio resultante das raízes dos termos iniciais pelo seu oposto: , logo a fatoração da diferença de dois quadrados é igual à raiz quadrada do primeiro termo menos a raiz quadrada do segundo termo vezes o oposto: , ou simplesmente .
Outros exemplos:
Fatoração do trinômio quadrado perfeito
editarConsidere o polinômio , que é um trinômio quadrado perfeito, pois representa , mas como saber se um trinômio é ou não quadrado perfeito?
Ainda considerando o polinômio , vamos obter a raiz quadrada do primeiro termo e a raiz quadrada do terceiro termo , finalmente multiplicamos por dois o produto das raízes para verificar se o resultado é igual ao segundo termo do polinômio (): , o resultado é igual ao segundo termo do polinômio, logo o mesmo é um trinômio quadrado perfeito e sua forma fatorada é .
Outro exemplo:
ou
Fatoração da soma ou da diferença de dois cubos
editarAs expressões usadas são:
Observe a multiplicação resolvida através da propriedade distributiva:
, tendo este cálculo como base, podemos dizer que , logo, a fatoração do polinômio é igual à raiz cúbica do primeiro termo , mais a raiz cúbica do segundo termo vezes o quadrado do primeiro termo , o produto dos dois termos com o sinal oposto mais o quadrado do segundo termo , formando:.
Outros exemplos:
Fatoração do trinômio do segundo grau
editarObserve o trinômio , cuja forma fatorada é , para realizar sua fatoração devemos obter dois números que somados dêem o coeficiente do segundo termo do polinômio (-2x) e multiplicados dêem o terceiro termo do polinômio (-35), e escrevê-los como produto de dois termos entre parênteses, veja outros exemplos:
Fatoração completa
editarA fatoração completa implica a união de todos os métodos de fatoração de polinômios para tornar um polinômio fatorado ao máximo, ou seja, que não pode ser mais fatorado. Considere o polinômio , que é a diferença de dois quadrados, fatorando-o temos: , note que o primeiro termo da fatoração [] é uma diferença de dois quadrados, devemos fatora-lo: , assim, temos a fatoração completa do polinômio .
Outros exemplos:
Fatoração por artifício
editarEm alguns casos, a fatoração só é possível com a utilização de algum artifício. Exemplo;
Fatore a expressão algébrica: .
Artifício utilizado: Adicionamos e subtraímos o termo , não alterando, assim, o valor da expressão e possibilitando a obtenção de trinômio quadrado perfeito para a realização da expressão.
Outro exemplo:
Artifício utilizado: soma-se e subtrai-se , obtendo-se logo em seguida uma soma de cubos:
Um passo intermediário que pode ser usado como artifício é a expressao da soma de dois quadrados:
Polinômios irredutíveis
editarAlguns polinômios não podem ser fatorados, estes são chamados de polinômios irredutíveis, mas o estudo destes polinômios deve ficar para um livro mais avançado.
Exercícios
editarProblemas resolvidos
editarCaso 1
editarUma indústria produz apenas dois tipos de camisas: o primeiro com preço de R$45,00 a unidade e o segundo com o preço de R$67,00 a unidade. Se chamarmos de x a quantidade vendida do primeiro tipo e de y a quantidade vendida do segundo tipo.
- Qual a expressão algébrica da venda desses dois artigos?
- Qual o valor se forem vendidos 200 e 300 unidades respectivamente?
Caso 2
editarO segundo caso de fatoração é: agrupamento, onde há 4 ou mais termos. Temos como exemplo:
- ax+ay+bx+by = a(x+y)+b(x+y)= (x+y)(a+b).
- Colocamos o 'x+y' em evidência e quem os multiplica também.
Caso 3
editarDiferença entre dois quadrados.
Caso 4
editarTrinômio quadrado perfeito.
Caso 5
editarSoma e produto
Caso 6
editarExercícios
editarFração algébrica
editarSimplificação
editar15x²-15xy²=15x(x-y²)
Operações
editarAdição
editarSubtração
editarMultiplicação
editarDivisão
editarReferências
editarWikipédia
editar
|
Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros. |
Polinômios
editarDefinição
editarPolinômios em uma variável são séries de monômios (ou termos) em uma variável, que por sua vez são expressões matemáticas na forma (que, no caso de n = 0, torna-se a constante a). Cada monômio é caracterizado por:
- um coeficiente, que na equação acima é representado por a;
- uma variável, que na equação é representada por x; e
- um expoente natural, que na equação é representado por n. No caso particular n = 0, considera-se que e o termo torna-se simplesmente a.
Assim, um polinômio é um conjunto de monômios, devidamente normalizados. A expressão mais correta é função polinomial, mas o uso de polinômio é consagrado. A função polinomial ou polinômio assume a forma:
A função constante, é um exemplo de função polinomial, bem como a função linear
Grau
editarDefine-se o grau de um polinômio como igual ao expoente mais alto entre as variáveis de seus monômios não-nulos. Por exemplo, no polinômio o grau é 3, correspondente ao expoente mais alto entre as variáveis nos monômios ().
Valor numérico
editarÉ o valor que se resulta a expressão quando determina-se um valor para as variáveis.
Exemplo
2x + 1 VN = ? Para x=5
VN = 2.5 + 1 = 11,
Raízes
editar
Raiz ou zero é um valor tal que, atribuído à variável da função polinomial, faz com que a função resulte em 0, ou seja, se a é dito raiz do polinômio P(x), então
Exemplos de raízes:
- tem raiz r = 4 (pois )
- tem raiz r igual a -1, pois
Um polinômio de grau n terá n raízes, sempre. Algumas vezes uma mesma raiz se repete, sendo por isso chamada raiz dupla, tripla, quádrupla, etc. Por exemplo:
- tem raiz dupla r igual a 2, uma vez que pode ser fatorado em
Num gráfico representativo da função polinomial, as raízes sempre ocorrem nos pontos em que a curva cruza o eixo das abcissas.
Obtenção de raízes
editarIdentidade de polinômios
editarDois polinômios são ditos idênticos se tiverem o mesmo grau e os monômios correspondentes idênticos, por exemplo:
Como o desenvolvimento de B(x) resultou num polinômio de termos correspondentes idênticos a A(x), então os polinômios são idênticos ou equivalentes; indica-se:
Polinômio nulo
editarUm polinômio é dito nulo quando todos os seus coeficientes são iguais a 0.
Igualdade de polinômios
editarDiz-se que os polinômios e são iguais quando para todo
Operações
editarAdição
editarConsideremos que tenhamos os fatores:
e
Todos constantes e com valores diferentes de zero.
Ainda temos:
que são variáveis.
Os polinômios:
e
A sua adição é efetuada como segue:
Em caso de polinômios compostos por mais de uma variável, tais quais:
e
A sua adição é efetuada como segue:
Processo:
Para fazer a soma dos polinômios de uma só variável, identificamos os monômios de mesmo expoente e somamos os fatores dos mesmos, o resultado da soma dos fatores é multiplicado pela parte variável do monômio, repete-se o processo para todos os monômios até que não haja mais fatores.
Para fazer a soma dos polinômios de várias variáveis, identificamos os monômios com variáveis iguais de mesmo expoente e somamos os fatores dos mesmos, o resultado da soma dos fatores é multiplicado pela parte variável do monômio, repete-se o processo para todos os monômios até que não haja mais fatores.
Subtração
editarO sinal de negativo (-)antes dos parêntese exige a troca de todos os sinais que estejam dentro dele.
(3x²-2x+5)-(5x-3)=
=3x²-2x+5-5x+3= =3x²-7x+8
Multiplicação
editar(15x² - 10x + 2) • (3x - 2)
Nesse caso, multiplica-se todos os termos ou considere:
- (15x² - 10x + 2) = A
- (3x - 2) = B
donde,
- A • B (ou B • A)
A •B --- x
donde,
(15x² - 10x + 2)
• (3x - 2)
-----------------
- 30x² + 20x - 4
45x³ - 30x² + 6x +
---------------------
45x³ - 60x² + 26x -4
Portanto, o produto da multiplicação indicada será 45x³ - 60x² + 26x -4.
Divisão
editarPara realizar-se uma divisão de polinômios, utiliza-se um dos teoremas abaixo:
- Método de Descartes
- Método do Resto
- Método de D'Alembert
- Método de Briot-Ruffini
Teoremas
editarTeorema do resto
editarO resto da divisão do polinômio P(x) por ax + b é dado por P(-b/a)
- Exemplo de resolução 1
- Têm-se a seguinte divisão:
- 1º passo: Determina-se x
-
- 2º passo: Substitui-se os valores
Portanto, o resto é 43.
- Exemplo de resolução 2
- O resto da divisão do polinômio pelo polinômio de primeiro grau é
Teorema de D'Alembert
editarUm polinômio é divisível pelo polinômio de primeiro grau se e somente se,
Aplicações práticas
editarEquações polinomiais
editarDefinição
editarTeorema Fundamental da Álgebra
editarTodo polinômio de uma variável com coeficientes complexos e de grau tem alguma raiz complexa. Em outras palavras, a equação polinomial tem soluções, não necessariamente distintas.
Apesar do nome pomposo, um estudo mais aprofundado da Álgebra contemporânea mostra que este resultado não é assim "tão fundamental". No entanto, no contexto das equações polinomiais, é ele quem traz a garantia de que existem soluções para esse tipo de equação.
Multiplicidade de uma raiz
editarRelações de Girard
editarTeorema das raízes complexas
editarFatoração
editar- Lembre-se: Fatorar é simplificar uma expressão a um produto.
Existem várias formas de se fatorar um polinômio, ou seja, escrevê-lo como um produto de expressões mais simples:
- fatoração simples (ou por evidência)
- fatoração por agrupamento
- trinômios do quadrado perfeito
- e outros
Fatoração simples (ou por evidência)
editarDestacam-se os termos em comum, e coloca-o em evidência, colocando entre parênteses as outras parcelas entre parênteses na forma de produto, multiplicando-o com o número em evidência
- Exemplo
- ax + ay + az = a (x + y + z)
Por agrupamento
editarAgrupam-se os termos em comum. Quando agrupamos os termos, fazemos evidência separadamente em cada agrupamento.
- Exemplo
- ax + by + bx + ay =
- ax + ay + bx + by =
- a (x + y) + b (x + y) =
- (x + y) • (a + b)
Trinômio do quadrado perfeito
editarEsse já é mais complexo, pois, partiremos em etapas explicando através do exemplo.
- Fatorar a expressão
Primeiro verificamos se é um Trinômio do quadrado perfeito:
- Extrai-se a raiz quadrada dos extremos. Com efeito,
- e
- Multiplicam-se os resultados
- 5 • m = 5m
- Multiplica-se o produto obtido por dois
- 5m • 2 = 10m
Note que 10m é o valor do meio na expressão, isso prova que ela é um Trinômio do quadrado perfeito.
- Sendo trinômio do quadrado perfeito
- Sendo Trinômio do quadrado perfeito, utiliza-se a fórmula substituindo-se os valores por ordem. O binômio representará uma adição caso o sinal do meio da expressão inicial for o sinal de mais (+), ou será uma subtração caso o sinal do meio da expressão inicial for o sinal de menos (-). Com efeito,
- (m - 5)²
Esse é o valor fatorado da expressão inicial.
Equação do segundo grau
editar- Lembre-se: Da fórmula ax² + bx + c .
A expressão abaixo se encaixa na fórmula acima.
- x² - 8x + 15
a (x - x1) • (x - x2)
Aplica-se a fórmula da fatoração das equações do segundo grau. Onde,
- x1 = 3
- x2 = 5
Por tanto, a fatoração de tal expressão resulta em:
- 1 (x - 3) • (x - 5)
- (x - 3) • (x - 5)
Exercícios
editarExercícios
editarA seguir são sugeridos alguns exercícios sobre fatoração de polinômios.
Fatore os seguintes polinômios:
Para fatorar os polinômios indicados nos próximos exercícios, é necessário conhecer a solução da equação do segundo grau:
Respostas
editarO leitor pode conferir as respostas dos exercícios anteriores digitando-as nos campos indicados e clicando em "Enviar". As respostas fornecidas utilizam o asterisco * para representar a multiplicação, ou então a simples justaposição das expressões. Devido a uma limitação do sistema utilizado na produção do questionário acima, pode acontecer que ele acuse incorretamente um erro quando sua resposta diferir da que foi indicada apenas por causa da ordem um termo da resposta. Em caso de dúvida, também pode conferir as respostas utilizando um dos diversos softwares de álgebra computacional existentes (se quiser uma uma lista de aplicativos deste tipo, pode consultar esta página da Wikipédia inglesa).
Por exemplo, com o programa Maxima consegue-se o resultado da fatoração de inserindo o comando
factor (3*a*x^2 - 18*a*x + 27*a);
Também é possível obter a resposta utilizando ferramentas gratuitas disponíveis na internet, como o Wolfram Aplha. Basta usar o mesmo comando factor seguido do polinômio que deseja fatorar, e a resposta é calculada em seguida. Veja as respostas para alguns dos exercícios acima, calculadas pelo Wolfram Alpha:
As respostas dos demais exercícios é obtida de maneira análoga.
Equações algébricas
editarDefinição
editarUma equação é uma igualdade de expressões matemáticas, que pode ser utilizada no estudo das funções, nomeadamente das suas raízes. Pelo menos uma da expressão contém uma ou várias incógnitas (variáveis), cujo valor é denominado de solução ou soluções da equação.
Cada uma das expressões pode ser considerada como função matemática (p.e. f(x) e g(x)), e partilhar as suas propriedades, em que cada operação efetuada sobre uma das expressões, terá que ser replicada na outra
Raiz
editarSe as equações forem polinomiais, i.e., compostas por polinômios, o grau n da equação é o mesmo que o maior expoente encontrado de ambos polinômios, e a sua solução admite no máximo n raízes. A raiz de uma equação é o valor com o qual a incógnita anula a equação.
Multiplicidade de raízes
editarNúmero de raízes de uma equação
editarRelações entre coeficientes e raízes, Equações algébricas com coeficientes reais - pesquisa de raízes racionais, raízes complexas conjugadas.
Exemplo
editarUm exemplo de como completar quadrado:
Temos a seguinte equação:
Agora imagine a equação:
Vamos tentar transformá-la em um quadrado da soma.
Perceba que
Esse menos 16 é para subtrair do 16 que se forma no produto notável de
,
é só isso, o método de completar quadrados é simplesmente você transformar os números em um quadrado da soma.
Casos particulares
editarEquação do 1º grau com 1 incógnita
editarSistemas do 1º grau
editarProblemas do 1º grau
editarA soma das idades de André e Carlos é 22 anos. Descubra as idades de cada um deles, sabendo-se que André é 4 anos mais novo do que Carlos.
Solução: Primeiro passamos o problema para a linguagem matemática. Vamos tomar a letra c para a idade de Carlos e a letra a para a idade de André, logo . Assim:
Resposta: Carlos tem 13 anos e André tem 13-4=9 anos.
Equação do 2º grau com 1 incógnita
editarAqui mostraremos como se pode deduzir a famosa fórmula para a resolução de equações do segundo grau, também conhecida como fórmula de Bhaskara.
Evolução
editar, donde
-
- a multiplica os termos:
-
- aqui tornou-se .
-
- aqui temos como X1 e como X2.
- então,
|
|
- por fim, e (x) é representado pela seguinte fórmula:
Exercícios
editarExercícios de aplicação da Fórmula de Bhaskara.
- Determine o conjunto solução, nos reais, das equações seguintes, usando a fórmula de Bhaskara
Exemplo 2 (2+X)(X+1)=2x+2+x.x+x
=x.x+3x+2=0
a=1
b=3
c=2
Aplicando na fórmula teremos:
Delta=b.b-4.a.c
Substituindo os valores na fórmula teremos: Delta=3×3-4×1×2 Delta =9-8 Delta=1
X1=-b+√delta/2.a
Substuindo history para x1.:
X1=-3+√1/2×1
X1=-3+1/2
X1=-2/2
X1=-1
X2=-b-√delta/2×a
X2=-3-√1/2×1
X2=-3-1/2
X2=-4/2
X2=-2
Equação frigate agradesso quem a very beijinho de Cristiamo
Sistemas do 2º grau
editarProblemas do 2º grau
editarNum jantar de confraternização, seria distribuído, em partes iguais, um prêmio de R$ 24.000,00 entre os convidados. Como faltaram 5 pessoas, cada um dos presentes recebeu um acréscimo de R$ 400,00 no seu prêmio. Quantos foram convidados a este jantar?
- Solução
x = número de convidados 24.000/x = prêmio recebido por cada um se não houvesse faltas 24.000/(x-5) = prêmio recebido por cada um, como faltaram 5 pessoas 24.000/x+400=24.000/(x-5) ===> cada um dos presentes recebeu mais 400 simplificando a equação: dividindo os termos por 400 60/x + 1 = 60/(x-5) mmc: entre x e x-5 = x.(x-5) 60 (x-5) + x.(x-5) = 60.x 60x - 300 + x² - 5x - 60x = 0 x²-5x-300 = 0 aplicando a fórmula de Bhaskara: x' = 20, x" = -15(raízes negativas não servem)
Resposta: 20 pessoas foram convidadas...
Equação biquadrada
editarUma equação biquadrada é um equação do quarto grau que não possuem termos de grau ímpar:
A técnica para resolver esta equação consiste em reescrever a equação como uma expressão em y de forma que:
Assim a equação biquadrada transforma-se numa equação do segundo grau em y:
Exercícios
editarVer Matemática elementar/Expressões algébricas/Equação biquadrada/Exercícios
|
Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros. |
Leitura complementar
editar- Gilberto G. Garbi. O Romance das Equações Algébricas. 3ª ed. São Paulo: Livraria da Física. 2009. ISBN 8588325764
- Gilberto G. Garbi. A rainha da Ciências: um passeio histórico pelo maravilhoso mundo da Matemática. Livraria da Física, 2006. ISBN 8588325616
Médias
editarEm Matemática, existem quatro tipos de médias.
- Média: a média de um conjunto de números é o valor numérico de tendência central que representa este conjunto.
Média Aritmética simples
editarÉ a razão entre a soma de todos os elementos de um conjunto e a quantidade de elementos deste conjunto.
- Matematicamente
- a + b + ... + z (n termos)
- Média aritmética simples →
Exemplo
editarA = {3,5,9,12} =
Média Aritmética Ponderada
editarÉ a razão do somatório dos produtos entre elementos e seu respectivo peso e, a soma dos pesos.
Exemplo
editar- João tirou 8 em Matemática e 9 em Português. Ele fará uma média Ponderada dando peso 3 à Matemática e peso 1 à Português. Qual será a média?
- PM → M=8 → PM=3
- PP → P=9 → PP=1
Média Harmônica
editarÉ o inverso da média Aritmética dos inversos dos números.
Exemplo
editar- 2 e 3
Média Geométrica
editarÉ a raiz n-ésima (ou enésima) do produto dos n números.
Exemplo
editar
Sistemas lineares
editarDefinição
editarSistemas lineares são conjuntos de equações lineares. Uma equação linear, por sua vez, é toda equação que pode tomar a forma:
- .
Por exemplo, 5x + 2y + z = 12 ou 0,2x - 15y = 0. Na equação linear sempre aparecem coeficientes e variáveis. No primeiro exemplo, os coeficientes são 5, 2 e 1 (implícito), e as variáveis são x, y e z.
As equações lineares podem ter um grupo de valores que, substituindo as variáveis, as tornam verdadeiras. Por exemplo:
O conjunto de valores (2,1,0) torna essa equação verdadeira:
Os valores que tornam a equação linear verdadeira são chamados soluções da mesma.
O sistema linear é composto por duas ou mais equações, geralmente apresentadas no seguinte formato:
Para estas equações pode haver um conjunto de valores que só serão a solução do sistema se forem solução de cada equação. Assim, no sistema:
Percebe-se que a solução única capaz de satisfazer a ambas as equações é o par (2,4). O sistema acima é chamado de sistema linear a 2 incógnitas, e portanto admite soluções que são pares ou duplas. De modo genérico, um sistema será linear a n incógnitas (ou variáveis) e terá por solução uma n-upla (lê-se "enupla") do tipo (α1, α2, α3, ... αn). Conforme veremos mais adiante, um sistema apresenta melhores condições de ser resolvido (ou seja, de ter sua solução encontrada) caso tenha um número de equações igual ao número de incógnitas.
Classificação
editarOs sistemas lineares podem ser classificados quanto a possibilidade de obtenção de soluções, dentro do conjunto numérico ao qual os sistemas devem ser resolvidos. Inicialmente, encontramos dois tipos de sistemas:
- impossíveis (ou inconsistentes) são os sistemas que não têm solução, geralmente por conterem equações lineares que se contradizem. Por exemplo:
- Observar que as equações apresentam o inconveniente de apresentar a mesma soma, mas com resultados diferentes, o que leva à impossibilidade de resolver o sistema. O sistema impossível (SI) sempre resulta numa contradição. Vale ressaltar que o conjunto numérico ao qual a solução pertence é fundamental na determinação da possibilidade do sistema; por exemplo:
- É considerado impossível dentro do conjunto dos números naturais, pois não há nenhum número natural que somado em dobro 2y a outro número natural x resulte em um valor menor do que ele próprio y somado ao mesmo número x. A solução real, (14,-2), é descartada se restringirmos a solução ao conjunto de números naturais (-2 não é natural).
- possíveis (ou consistentes) são todos os sistemas que não levam a uma contradição, e portanto admitem soluções dentro do conjunto numérico ao qual estão designados. Os sistemas possíveis, por sua vez, se subdividem em dois tipos:
- possíveis determinados (SPD) são os sistemas que possuem apenas uma solução; é possível identificar uma n-upla capaz de resolver todas as equações, única. Como exemplo, além daquele citado na seção anterior, o sistema:
- Permite como solução real a dupla (-6, 8).
- possíveis indeterminados (SPI) são os sistemas que permitem infinitas soluções, porque apresentam os chamados graus de liberdade, ou seja, permitem soluções arbitrárias. Por exemplo, o sistema:
- Permite uma infinidade de soluções como (10,2), (12,4), (19,11), etc. Em todas elas, basta que a relação entre o primeiro elemento e o segundo seja (α,α - 8). Também é indeterminado o sistema:
- Pois apresenta mais incógnitas do que equações, sendo por isso impossível "trabalhar" as incógnitas de modo a obter valor preciso para cada uma. A solução é qualquer tripla do tipo (α, 8 - α, -2). Observar que o terceiro elemento pode ser definido, mas não os dois outros, de modo que essa é a mesma situação do sistema indeterminado do exemplo anterior.
Sistemas equivalentes
editarDiz-se que dois sistemas lineares são equivalentes se, e somente se, apresentam a(s) mesma(s) n-upla(s) como solução(ões). Assim, os sistemas:
- E
- Ambos apresentam como solução (-1, 2). Ambos são sistemas equivalentes, portanto.
Um sistema equivalente constitui, de certo modo, apenas um desenvolvimento de outro sistema, das equações desse outro sistema devidamente transformadas. A relação de equivalência está presente desde situações mais óbvias (quando dois sistemas são em tudo iguais, exceto pela ordem das equações lineares, por exemplo) até situações mais complexas, nas quais é preciso multiplicar e somar as equações para obter as mesmas equações de outro sistema. No exemplo dado, o segundo sistema foi formado a partir de duas equações:
- é a subtração de por
- é a subtração de por
A equivalência de sistemas é fundamental para transformação dos mesmos, e eventual resolução por método de escalonamento, que será discutido mais adiante.
Resolução de sistemas
editarOs sistemas lineares podem ser resolvidos (ou seja, ter a solução encontrada) através de diferentes métodos. Aqui examinar-se-á o método de escalonamento, e no próximo capítulo, o método ou regra de Cramer, que utiliza-se de matrizes.
O método do escalonamento permite resolver sistemas lineares de n equações a n incógnitas. Caso existam mais incógnitas do que equações, o método não funcionará, ou seja, ele não permite resolver sistemas com grau de liberdade maior ou igual a 1. Já os sistemas com mais equações do que incógnitas podem ser resolvidos, desde que não hajam contradições que o tornem SI.
Escalonamento
editarClassificado o sistema como SPD ou SPI, pode ser feito o escalonamento, que consiste basicamente em deixar as equações do sistema na forma:
Ou seja, o sistema deve ter diversas equações, cada uma com um número crescente ou decrescente de incógnitas, de modo que a última se reduza a apenas uma incógnita. Isso é feito com as transformações adequadas – sempre é possível "zerar" uma das incógnitas na equação pela soma/subtração da equação anterior que contenha essa incógnita. Exemplificando:
Inicialmente, vamos eliminar o termo composto pela variável x nas duas últimas equações, a partir da primeira. Para tanto, inicialmente multiplicamos a segunda equação por -2 e a terceira por 4. Depois, somamos as equações a primeira e obtemos:
A continuar o processo, pode-se trabalhar a segunda e a terceira equação linear para obter na terceira uma equação a uma variável, que arbitrariamente escolhemos ser z. Para tanto, vamos multiplicar a segunda equação por -3, e então somá-la à terceira equação:
A partir desta última equação, e em geral em qualquer sistema resolvido por escalonamento, é possível encontrar o valor de uma primeira variável, no caso específico:
Substituindo o valor encontrado para z na equação da segunda linha, temos:
Por fim, é possível substituir esses dois valores na primeira equação:
A solução do sistema é, portanto, (-4,1,1).
Assim resolvem-se os sistemas lineares pela técnica do escalonamento: progressivamente vão obtendo-se os valores das variáveis, até que todas as equações possam ser resolvidas. Trata-se de um método prático, que inclusive é utilizado em computadores para resolução de sistemas lineares (embora o enfoque computacional seja um tanto mais complicado e envolva matrizes).
Sistemas com grau de liberdade
editarÉ usado na estatística
Método de Gauss
editarO método de Gauss é um método geral de resolver sistemas de equações lineares, consistindo de uma sequência de passos simples que reduzem o sistema até que a solução se torna óbvia.
|
Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros. |
Sistemas de equações algébricas
editarDefinição
editarSistemas de equações algébricas são conjuntos de equações algébricas. Em tais equações, admite-se qualquer operação matemática. Por exemplo, em
ocorre o produto de variáveis.
Diferentemente de um sistema de equações lineares (formado por linhas - retas), nas equações algébricas os gráficos têm inúmeras formas. Estes apresentam essencialmente curvas, e podem ter várias soluções. O número de soluções de um sistema de equações algébricas é dado pelo número de intersecções que existem num gráfico. Exemplos:
Resolução
editarA solução de um sistema com duas equações são as coordenadas das intersecções nos gráficos. Portanto, a solução de x e y em um sistema qualquer é (x, y) da intersecção. Para um sistema com três variáveis, pode-se considerar um terceiro plano z para o gráfico.
Para determinar tais coordenadas, utiliza-se o método da substituição. Por exemplo, no sistema
isola-se uma das variáveis:
Em seguida, substitui-se este novo resultado na equação seguinte:
Eliminada uma variável, pode-se descobrir o valor da primeira:
Para descobrirmos o valor de y, neste caso, utilizaremos a famosa fórmula de Bhaskara:
Substituiremos y por tais valores na primeira equação:
Assim, temos duas soluções para este sistema: (2; 3) e (3; 2).
Sistemas com várias equações
editarUm sistema com n equações pode possuir até n variáveis para que se possa determinar o valor de cada incógnita. Nestes casos, as intersecções devem ocorrer entre todas as equações envolvidas. Exemplo:
Primeiramente, isolaremos uma incógnita em uma das equações. Optaremos pela primeira equação, por ser mais simples. Também, resolveremos a terceira equação:
Substituiremos a incógnita isolada x por -y nas demais equações:
Realizando a fórmula de Bhaskara, obteremos as raízes 0 e 1 na segunda equação. Na terceira, teremos 0 e -2. Já que a solução de um sistema é a intersecção dos gráficos, as raízes devem repetir em todas as equações. Portanto, a única raiz compatível é zero. Substituiremos os resultados compatíveis (neste caso, zero) em uma equação qualquer. Optaremos pela primeira:
Assim, obtivemos o primeiro par ordenado: (0; 0). Agora, substituiremos a incógnita -y por x (ou y por -x) na segunda e na terceira equação:
Através da fórmula de Bhaskara, obteremos as raízes 0 e -1 na segunda e na terceira equação. Deste modo, ambos os resultados são compatíveis. Pelo fato de já termos substituído 0 na primeira equação no processo anterior (em que se descobriu o primeiro par ordenado), resta apenas substituir por -1. Optaremos, novamente, pela primeira equação:
Conclui-se que (-1; 1) também é uma solução do sistema.
Exercícios
editar
|
Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros. |
Equações irracionais
editarUma equação irracional é uma equação onde existem polinômios e raízes.
Por exemplo:
Uma definição mais precisa seria: uma equação algébrica irracional é uma equação onde existem funções racionais e inversas de funções polinomiais.
Solução
editarUm dos métodos de solução é isolar, em um dos membros da equação, os termos que incluem raízes, e elevar ambos os membros a uma mesma potência que elimine a raiz. No entanto, este procedimento não produz uma equação equivalente a original, mas sim uma equação que possui entre as suas soluções os valores que resolvem a equação inicial.
Por exemplo, quando se tem a igualdade entre uma certa expressão e outra expressão , pode-se concluir que Por outro lado, é perfeitamente possível que duas expressões tenham os quadrados iguais, sem que elas próprias sejam iguais. Este é o caso, por exemplo, quando se tem , pois para a maioria dos números, (a igualdade só vale para ). Assim, se durante a resolução ambos os membros forem elevados a uma certa potência, será necessário checar se os valores obtidos como solução para a nova equação são também soluções da equação inicial.
Acompanhe o próximo exemplo:
Isolando a raiz, elevando ao quadrado e resolvendo:
Esta equação do segundo grau possui duas soluções, a saber: e . Isto não significa que ambos estes números sejam soluções da equação original, pois com os cálculos realizados até agora só é possível dizer que "se for uma solução para a equação original, então tem que ser igual a ou igual a ".
Resta então saber se algum destes números verifica a equação proposta:
- , logo 3 também é uma solução da primeira equação.
- , logo 0 não é uma solução da equação inicial.
Portanto, a única raiz é "x = 3
Exercícios
editar
|
Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros. |
Matrizes
editarMatrizes
editarConceito
editarUma matriz pode ser entendida como um conjunto de mn (m multiplicado por n) números, dispostos em m linhas e n colunas, conforme figura ao lado.
Notação
editar- Matrizes devem ser escritas com parênteses ou colchetes à esquerda e à direita, sendo as duas maneiras equivalentes.
- Uma matriz é indicada por uma letra maiúscula.
- Seus elementos são indicados usando a mesma letra, porém minúscula, com a linha e coluna usados como índice (nesta ordem). Assim, o elemento da 3ª coluna na 2ª linha da matriz A será .
Assim, na matriz acima, de 2 linhas e 3 colunas, temos:
Ordem de uma matriz
editarOrdem de uma matriz refere-se ao seu número de linhas e colunas. É apresentada na notação m×n, onde m é o número de linhas e n o de colunas. Lê-se "m por n".
Assim, a matriz A acima é de ordem 2×3.
Adição e subtração
editarEsta operação só pode ser feita com matrizes de mesmo número de linhas e mesmo número de colunas (mesma ordem). Sejam duas matrizes e .
Então a matriz é uma matriz mn tal que cada elemento de é dado por:
- . Ver exemplo ao lado.
Multiplicação por um escalar
editarSeja a matriz e um escalar. A matriz
é uma matriz m×n tal que cada elemento de é dado por:
- .
Algumas propriedades das operações anteriores
editarSejam e matrizes e e escalares. Então:
e .
E, também, se e então .
Matrizes nulas
editarMatriz nula é aquela cujos elementos são todos nulos.
matriz identidade é matriz na qual se e zero nos demais casos. Ou, de outra maneira, é a matriz na qual todos os elementos da diagonal principal são iguais a 1 e os demais são nulos.
Matrizes especiais
editar- Matriz linha é a matriz em que o número de linhas é igual a 1.
- Matriz coluna é a matriz em que o número de colunas é igual a 1.
- Matriz quadrada é a matriz em que o número de linhas é igual ao número de colunas.
- Matriz unitária é a matriz em que obedece a relação ().
- Matriz transposta () da matriz é a matriz obtida pela permutação das linhas e colunas de . Ou seja, cada coluna de será uma linha de e cada linha da matriz original será uma coluna da transposta.
Multiplicação de matrizes
editarSejam as matrizes e (o número de colunas da primeira deve ser igual ao número de linhas da segunda).
O produto AB é dado pela matriz cujos elementos são calculados por:
e
Veja os cálculos para o exemplo da figura acima.
Ordem dos fatores
editarSe A e B são matrizes quadradas (igual número de linhas e colunas), ambos os produtos AB e BA podem ser calculados.
Entretanto, na multiplicação de matrizes, a ordem dos fatores não é indiferente. Em geral, .
Se AB = BA, as matrizes são ditas comutativas......
Algumas propriedades do produto de matrizes
editarSejam as matrizes A, B e C.
- Se os produtos A(BC) e (AB)C são possíveis de cálculo, então A(BC) = (AB)C.
- Se os produtos AC e BC são possíveis, então (A+B)C = AC + BC.
- Se os produtos CA e CB são possíveis, então C(A+B) = CA + CB.
- Se é a matriz unitária conforme já mencionado, então: e .
Matriz inversa
editarSejam as matrizes quadradas e .
Se , onde é a matriz unitária conforme já visto, então B é chamada de matriz inversa esquerda de A.
Para achar a matriz inversa:
Por exemplo, seja a matriz A ao lado e desejamos saber sua inversa esquerda B. O primeiro passo é acrescentar uma matriz unitária no lado direito de A.
Agora, o objetivo é somar ou subtrair linhas multiplicadas por coeficientes de forma a obter a matriz unitária no lado esquerdo (processo de Gauss-Jordan).
- 1ª linha = 1ª linha + 2ª linha multiplicada por -1.
- 2ª linha = 2ª linha + 1ª linha multiplicada por -1.
- 3ª linha = 3ª linha + 1ª linha multiplicada por -2.
- 3ª linha = 3ª linha + 2ª linha multiplicada por -3.
- 3ª linha = 3ª linha multiplicada por -1.
- 2ª linha = 2ª linha + 3ª linha multiplicada por -1.
E a matriz inversa é a parte da direita.
Determinantes
editarDeterminantes de 2ª ordem
editarO conceito de determinante está ligado ao de matriz, embora seja completamente distinto: enquanto matriz é o conjunto de elementos conforme já mencionado, determinante é o resultado de uma operação aritmética com todos os elementos de uma matriz, que obedece a uma determinada regra. Só se aplica a matrizes quadradas.
O prefixo det é colocado antes da matriz para indicar determinante. Ou, de forma mais compacta, os colchetes na matriz são substituídos por barras verticais para o mesmo efeito.
Para calcular um determinante de uma matriz (determinante de 2ª ordem):
Seja . Então
Determinantes de ordens superiores
editarPara determinantes de 3ª ordem, há um método conhecido como regra de Sarrus. Considere a matriz:
Exemplo para 3ª ordem.
Quando a ordem é superior a 3, não há algoritmos simples a ponto de poderem ser generalizados por uma fórmula. Há, no entanto, dois métodos de decomposição que reduzem um determinante a determinantes de ordens menores. Um deles é conhecido como Teorema de Laplace, e vale para qualquer matriz. Outro método, mais simples, é a regra de Chió, mas há algumas restrições para que ele funcione numa matriz.
Regra de Chió
editarTeorema de Laplace
editarO Teorema de Laplace permite expandir um determinante de ordem em uma soma de determinantes de ordem . A descrição do procedimento é a seguinte:
Considera-se uma fila (linha ou coluna) qualquer da matriz; somam-se os produtos de cada elemento desta linha por seus respectivos cofatores. O cofator de um elemento, por sua vez, é definido como o determinante da matriz que resta da eliminação da linha e coluna que passam pelo elemento, multiplicado pelo fator sinal ― negativo se a soma do índice da coluna com o índice da linha for ímpar, e positivo do contrário. O processo pode ser repetido indefinidamente, até chegarmos num determinante que possa ser calculado trivialmente.
Para deixar o processo mais claro, considere uma matriz . Podemos escolher qualquer linha ou coluna para calcular o determinante; vamos, por comodidade, escolher a segunda coluna, pois ela contém um zero ― o que nos dispensa de calcular um determinante, já que este seria multiplicado por zero. Então
Você pode verificar que esse mesmo valor será obtido se usarmos a expansão de Laplace por outra coluna ou linha, e também se usarmos a regra de Sarrus. De fato, podemos provar, algebricamente, que a regra de Sarrus é equivalente ao uso do teorema de Laplace para um determinante de ordem 3.
Algumas propriedades dos determinantes
editar- Mantidas as ordens dos elementos, um determinante não se altera se linhas e colunas são trocadas (ou seja, ).
- Se duas linhas ou duas colunas são trocadas entre si, o determinante muda de sinal.
- Se os elementos de duas linhas ou colunas são iguais entre si ou proporcionais entre si, o determinante é nulo. Se uma das linhas ou colunas contiver apenas zeros, o determinante também será nulo. Mais genericamente, o determinante é nulo se uma fila for uma combinação linear das outras filas.
- Se os elementos de uma mesma linha ou coluna têm um fator de multiplicação comum, ele pode ser colocado em evidência.
- Generalizando a propriedade anterior, se uma matriz n x n tiver todos elementos multiplicados por k, então seu determinante será multiplicado por kn
- Um determinante não se altera se aos elementos de uma linha ou coluna são somados ou subtraídos os elementos (ou múltiplos deles) de outra linha ou coluna.
- O determinante de uma matriz é igual ao da sua transposta
- Ao trocarmos duas linhas ou colunas, o valor do seu determinante é multiplicado por (-1)
- O determinante de uma matriz triangular é igual ao produto os elementos da diagonal
- O determinante do produto de duas matrizes é igual ao produto dos determinantes destas matrizes (Teorema de Binet)
Exemplo de aplicação de determinantes
editarSeja o sistema de equações lineares
e o determinante
e os determinantes , e , obtidos substituindo-se, respectivamente, as colunas dos coeficientes de , e pela coluna dos termos independentes:
Então a solução do sistema é dada por:
Esse método costuma ser chamado de método de Cramer.
Ver também
editar- Álgebra linear/Matrizes (livro com conteúdo mais avançado)
Análise combinatória
editarAnálise combinatória
editarAnálise combinatória é a parte da matemática que estuda os métodos de contagem.
A operação fatorial
editarA função fatorial é uma função que admite apenas um único argumento. Para esse argumento, chamemos-lhe , a função fatorial procura todos os números menores ou iguais a e maiores que e multiplica-os entre si. Adicionalmente, é preciso dizer que tanto como pertencem ao conjunto dos números naturais (com uma pequena diferença, inclui o número zero, não) e que a função fatorial é representada pelo símbolo/operador (ponto de exclamação). Definindo tudo isto formalmente:
Mas esta função ainda não nos diz muito acerca do que é de o fatorial de um número, diz-nos apenas como a representar e qual o seu domínio. Assim, não nos é possível saber para um dado valor qual o valor de .
A definição correta de fatorial é dada pelo operador produtório da seguinte forma:
Note-se que aqui o valor já não é incluído como um possível valor de .
Isto significa precisamente aquilo que já foi dito antes. Neste caso, a função produtório começa por atribuir a o valor de ; de seguida, vai multiplicar esse mesmo valor pelo próximo valor de , ou seja, ; esta operação repete-se até que o valor de seja igual ao valor de . Dito isto, uma forma mais simples de definir a função fatorial seria:
Embora a definição mais utilizada seja:
Estas duas definições são exatamente iguais, apenas muda a ordem pela qual as parcelas aparecem.
Exemplos
editarou
mas
Acontece que, embora esta função não esteja definida para , foi estipulado que o fatorial do número zero é um. Portanto:
O que equivale a dizer "0 fatorial está definido como sendo 1".
Operações com fatoriais
editarSe reparar nos exemplos anteriores, não é mais do que , o que já nos indica uma operação relativa a fatoriais: a fatorização.
Ainda outra maneira de definir a função fatorial, é utilizar uma função recursiva:
ou, por outro lado:
Princípio fundamental da contagem
editarSe um determinado acontecimento ocorre em n etapas diferentes, e se a primeira etapa pode ocorrer de p1 maneiras diferentes, a segunda de p2 maneiras, a terceira de p3 maneiras, até pn, o número total de maneiras de ocorrer o acontecimento é :
T = p1 × p2 × p3 × ...× pn ×
Ex.: Se tivermos um dado de 4 faces e um de 6 faces, logicamente, o primeiro pode apresentar 4 resultados diferentes, e o segundo, 6. Os dois juntos podem apresentar, então, 6*4=24 resultados diferentes.
Permutações simples
editarPermutações são os agrupamentos de um determinado número de elementos variando apenas a sua ordem. Ex.:
XYZ, XZY, YXZ, YZX,ZXY, ZYX. O número de agrupamentos de uma permutação simples de n elementos é dado por n!.
Ex.: De quantas formas podemos agrupar as sete cores do arco-íris? R: 7! = 5040
Permutações com elementos repetidos
editarSe formos fazer permutações com n elementos, mas existe um elemento repetido 'a' vezes, outro 'b' vezes, outro 'c' vezes, etc, o número de possibilidades de permutações é:
Pn(a,b,c) = n! / (a! b! c!)
Determine o número de anagramas (combinações de letras formando palavras com ou sem sentido) que podemos formar com PATA. E com MACACA. R: P1= 4!/2! = 12 P2= 6!/(3!*2!) = 60
Obs.: Exemplos de anagramas com PATA: AAPT, AATP, APTA, ATPA, PTAA, TPAA, PATA, TAPA, APAT, ATAP, PAAT, TAAP.
Arranjos simples
editarImagine que temos um conjunto de 'n' elementos. O arranjo simples de taxa 'K' é todo agrupamento de 'K' elementos distintos, podendo variar a ordem em que aparecem.
Ex.: A={X,Y,Z}
arranjo de taxa 1: X,Y,Z. arranjo de taxa 2: XY, YX, XZ, ZX, YZ, ZY. arranjo de taxa 3: XYZ, XZY, YXZ, YZX, ZXY, ZYX.
O número total de arranjos de 'n' elementos, taxa 'K' é:
Quantos anagramas de três letras podemos formar pelo nosso alfabeto (com 26 letras)? Resposta:
Combinações simples
editarAs combinações são parecidas com os arranjos, mas apenas há a preocupação com a existência do elemento (não com a ordem). Ex.:
Combinações de taxa 1 do conjunto A={A,B,C,D} A, B, C, D.
Combinações de taxa 2 do conjunto A={A,B,C,D} AB, AC, AD, BC, BD, CD.
Combinações de taxa 3 do conjunto A={A,B,C,D} ABC, ABD, ACD, BCD.
Combinações de taxa 4 do conjunto A={A,B,C,D} ABCD.
A fórmula é:
Ex.: Um jogo possui um cartão com 60 números. Deve-se marcar 6 deles. De quantas forma pode-se fazer isso? Resposta:
|
Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros. |
Probabilidade
editarA palavra probabilidade origina-se do Latim probare (provar ou testar). Informalmente, provável é uma das muitas palavras utilizadas para eventos incertos ou conhecidos, sendo também substituída por algumas palavras como “sorte”, “risco”, “azar”, “incerteza”, “duvidoso”, dependendo do contexto.
Noção e distribuição de probabilidades
editarProbabilidade condicional
editarAo lançar uma moeda, sob certas condições, podemos calcular, com certeza a velocidade com que ela atingirá o solo. Repetindo esse lançamento nas mesmas condições, obtemos o mesmo resultado. Os experimentos em que podemos determinar os resultados nas diversas vezes que repetimos são denominados experimentos determinísticos.
Contudo, se observarmos um outro aspecto do mesmo lançamento e quisermos determinar qual das faces da moeda cairá voltada para cima, não conseguiremos determinar com clareza se sairá cara ou coroa, pois, em lançamentos sucessivos e em condições idênticas podemos descrever todos os resultados possíveis (no caso da moeda, cara ou coroa).
Experimentos que têm essa característica são chamados experimentos aleatórios. Por exemplo:
- Lançar um dado e observar a face virada para cima.
- Retirar e observar uma carta de um baralho.
- Sortear uma bolinha no bingo e verificar o número.
Eventos independentes
editar|
Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros. |
Geometria plana
editar|
Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros. |
Tópicos
editar- Conceitos geométricos
- Ângulos
- Retas no plano
- Triângulos
- Polígonos
- Circunferência e círculo
- Construções geométricas usando régua e compasso
- Áreas e volumes
Conceitos geométricos
editarGeometria plana
editarConceitos geométricos primitivos
editarA Geometria Plana e a Geometria Espacial baseiam-se nos chamados conceitos geométricos primitivos. Define-se como conceito primitivo toda aquele que não admite definição, isto é, o conceito que é aceito por ser óbvio ou conveniente para uma determinada teoria. Normalmente, em Matemática, os conceitos primitivos servem de base para a construção de postulados (ou axiomas) que formarão, por sua vez, a estrutura lógica e formal da teoria.
Ao contrário do que se pensa, conceitos primitivos existem não somente em Matemática, mas em Física também. Exemplos desses conceitos são os conceitos de força e velocidade.
Os conceitos geométricos primitivos são os seguintes:
- Ponto: é o conceito geométrico primitivo fundamental. Euclides o definiu como "aquilo que não tem parte". Ou seja, para Euclides é o conceito de "parte", e não de "ponto", que é primitivo.
- Imagine o ponto o menor que você puder. Diz-se que o ponto não tem dimensão (é adimensional), ou seja, ele é tão ínfimo quanto quisermos, e não faz sentido mencionar qualquer coisa sobre tamanho ou dimensão do ponto. A única propriedade do ponto é a localização.
- Representa-se o ponto por uma letra maiúscula qualquer do alfabeto latino.
- Linha: Imagine um pedaço de barbante sobre uma mesa, formando curvas ou nós sobre si mesmo: este é um exemplo de linha.
- Reta: É uma linha infinita e que tem uma única direção. Uma reta é o caminho mais curto entre dois pontos quaisquer.
- Superfície:
- Plano: Você pode imaginá-lo como uma folha de papel infinita. Um plano é uma superfície plana que se estende infinitamente em todas as direções.
Lugar Geométrico
editarLugar geométrico é um conjunto de pontos que satisfazem uma determinada propriedade. Nem mais, nem menos!
No contexto da geometria analítica, a propriedade geralmente pode ser descrita por uma equação. Nesse sentido, um lugar geométrico pode ser entendido como um conjunto de pontos onde determinada função é igual a zero (ou seja, sua curva de nível zero). Um estudo mais aprofundados dos conjuntos de pontos dados por uma equação, a relação entre conjuntos deste tipo, e outros problemas similares são estudados em uma área da matemática denominada geometria algébrica.
Exemplos: ... Circunferência
Reta
editarReta é uma noção primitiva.
Semi-reta
editarEnquanto a reta é infinita para os dois lados, a semi reta é infinita numa direção e finita na outra.
Segmento de reta
editarEnquanto a reta é infinita para os dois lados o segmento de reta termina em ambos os lados, ou seja, a menor distância entre dois pontos em um plano.
Áreas
editarA área de uma superfície plana é um número que expressa o tamanho daquela superfície. Quando maior, maior a área. Existe uma definição formal. É a seguinte:
A área de uma superfície é um número real positivo de forma que:
- A superfícies equivalentes estão relacionadas áreas iguais
- A área da soma de superfícies é a soma das áreas das superfícies
- Se uma superfície está contida em outra, sua área é menor ou igual à área da outra.
Ângulos
editarÂngulo
editarIntuitivamente, o ângulo é uma medida que expressa o quanto dois segmentos de reta estão não-paralelos.
|
Esta página é um esboço de geometria. Ampliando-a você ajudará a melhorar o Wikilivros. |
Retas no plano
editarParalelas
editar- Possuem coeficientes angulares iguais;
- Se interceptam no infinito (nunca se encontram).
Perpendiculares
editar- Possuem inclinação de 90° entre si;
- Se interceptam em apenas um ponto P definido na solução do sistema composto pelas equações das duas retas.
- Sendo a e b os coeficientes angulares de duas retas perpendiculares, a = - (b-1).
Feixe de paralelas cortadas por transversais
editar- Em cada paralela: Ângulos opostos pelo vértice: Equivalentes;
Teorema de Tales
editar
O Teorema de Tales foi proposto pelo filósofo grego Tales de Mileto, e afirma que: quando duas retas transversais cortam um feixe de retas paralelas, as medidas dos segmentos correspondentes determinados nas transversais são proporcionais. Para entender melhor o Teorema de Tales, é preciso saber um pouco sobre razão e proporção. Para a resolução de um problema envolvendo o Teorema de Tales, utiliza-se a propriedade fundamental da proporção, multiplicando-se os meios pelos extremos. Considerando-se o exemplo da figura, tem-se:
Aplicação do Teorema de Tales
editarO Teorema de Tales pode ser aplicado em triângulos que possuem uma reta paralela a um dos lados.
Veja também
editarTriângulos
editarTipos de triângulos
editarClassificação segundo a medida relativa dos lados
editarUm triângulo pode ser classificado de acordo com as medidas relativas de seus lados:
- Um triângulo equilátero possui todos os lados congruentes. Pode-se verificar que um triângulo eqüilátero é também eqüiângulo, ou seja, possui todos os seus ângulos internos congruentes (e com medida 60°). Por este motivo, este tipo de triângulo é também um polígono regular.
- Um triângulo isósceles possui pelo menos dois lados congruentes. Num triângulo isósceles, o ângulo formado pelos lados congruentes é chamado ângulo do vértice. Os demais ângulos denominam-se ângulos da base e, como se pode verificar, são congruentes. Note que os triângulos equiláteros também são isósceles.
- Em um triângulo escaleno, as medidas dos três lados são diferentes. É possível mostrar que os ângulos internos de um triângulo escaleno também possuem medidas diferentes.
Denomina-se base o lado sobre qual apóia-se o triângulo. No triângulo isósceles, considera-se base o lado de medida diferente.
A seguir é mostrada a classificação de alguns triângulos de acordo com o critério anterior:
Exemplo de triângulo equilátero
editarEste triângulo é equilátero, pois possui os três lados congruentes. Em particular, como seus lados são dois a dois congruentes, ele é um triângulo isósceles. Pode-se observar que seus todos os seus ângulos internos medem 60°, e por isso ele é equiângulo.
Exemplo de triângulo isósceles
editarNeste triângulo há somente dois lados congruentes: os que têm medida . Por este motivo, o triângulo é isósceles, mas não é equilátero. Além disso, cada um destes dois lados forma um ângulo de medida com a base do triângulo.
Exemplo de triângulo escaleno
editarAqui, cada um dos lados tem um comprimento diferente dos demais. Assim, este é um triângulo escaleno. Observe ainda que nenhum par de ângulos internos tem a mesma medida.
Classificação de acordo com seus ângulos internos e externos em baixo
editarUm triângulo também pode ser classificado de acordo com seus ângulos internos:
- Um triângulo retângulo possui um ângulo reto. Num triângulo retângulo, denomina-se hipotenusa o lado oposto ao ângulo reto. Os demais lados chamam-se catetos. Os catetos de um triângulo retângulo são complementares.
- Um triângulo obtusângulo possui um ângulo obtuso e dois ângulos agudos.
- Em um triângulo acutângulo, todos os três ângulos são agudos.
Exemplo de triângulo retângulo
editar- Um ângulo reto, ou seja, um ângulo de 90º.
Exemplo de triângulo obtusângulo
editar- Um ângulo obtuso e dois ângulos agudos.
Exemplo de triângulo acutângulo
editar- Todos os três ângulos são agudos. Ou seja, menor que 90º
Soma dos ângulos internos
editarNa geometria euclidiana, de acordo com o teorema angular de Tales, a soma dos ângulos internos de qualquer triângulo é igual a dois ângulos retos (180° ou π radianos). Isso permite a determinação da medida do terceiro ângulo, desde que sejam conhecidas as medidas dos outros dois ângulos.
Soma dos ângulos externos
editarExiste também um corolário, que afirma que a medida de um ângulo externo de um triângulo é igual à soma das medidas dos ângulos internos não-adjacentes.
Exemplo: Se os ângulos internos de um triângulo forem: a resposta final será assim: Resolução: , . Porque o ângulo externo é a igual à soma dos ângulos internos duas vezes.
Relações de desigualdades entre lados e ângulos
editar1ª relação: Um ângulo externo de um triângulo é maior que qualquer um dos ângulos internos não-adjacentes.
2ª relação: Se dois lados de um triângulo tem medidas diferentes, ao maior lado opõe-se o maior ângulo e ao menor lado, opõe-se o menor ângulo.
3ª relação: Em todo triângulo, qualquer lado tem medida menor que a soma das medidas dos outros dois.
Área do triângulo
editarExistem várias formas de se expressar a área A de um triângulo:
- Dadas a base b e a altura h:
- Dados dois lados a e b e o ângulo γ entre eles compreendido:
- Dados os três lados a, b e c: , onde p é o semiperímetro (metade do perímetro). Essa fórmula é conhecida como fórmula de Heron.
Se o triângulo for equilátero de lado L, sua área pode ser obtida pela fórmula:
Congruência
editarCritério LLL
editarLado-Lado-Lado.
Critério LAL
editarLado-Ângulo-Lado.
Critério ALA
editarÂngulo-Lado-Ângulo.
Critério LLAr
editarLado-Lado-Ângulo reto.
Semelhança
editarCritério LLL
editarSegundo o critério LLL (lado-lado-lado), existe semelhança entre dois triângulos se os três lados de um são proporcionais aos três lados correspondentes do outro.
Critério LAL
editarSegundo o critério LAL (lado-ângulo-lado), existe semelhança entre dois triângulos se têm entre si dois pares de lados correspondentes proporcionais e se os ângulos por eles formados forem iguais.
Critério AA
editarSegundo o critério AA (ângulo-ângulo), existe semelhança entre dois triângulos se eles têm dois ângulos iguais.
Referências
editarVer também
editar
|
Esta página é um esboço de geometria. Ampliando-a você ajudará a melhorar o Wikilivros. |
Pontos, linhas e círculos associados a um triângulo
editarPontos, linhas e círculos associados a um triângulo
editarMediatriz
editar
A mediatriz é a reta perpendicular a um lado do triângulo, traçada pelo seu ponto médio. As três mediatrizes de um triângulo se encontram em um único ponto, o circuncentro, que é o centro da circunferência circunscrita ao triângulo, que passa pelos três vértices do triângulo. O diâmetro dessa circunferência pode ser achado pela lei dos senos.
O Teorema de Tales determina que se o circuncentro estiver localizado em um lado do triângulo, o ângulo oposto a este lado será reto. Determina também que se o circuncentro estiver localizado dentro do triângulo, este será acutângulo; se o circuncentro estiver localizado fora do triângulo, este será obtusângulo.
Altura
editar
Altura é um segmento de reta perpendicular a um lado do triângulo ou ao seu prolongamento, traçado pelo vértice oposto. Esse lado é chamado base da altura, e o ponto onde a altura encontra a base é chamado de pé da altura.
O ponto de interseção das três alturas de um triângulo denomina-se ortocentro (H). No triângulo acutângulo, o ortocentro é interno ao triângulo; no triângulo retângulo, é o vértice do ângulo reto; e no triângulo obtusângulo é externo ao triângulo. Os três vértices juntos com o ortocentro formam um sistema ortocêntrico.
A formula para determinar a área do triângulo é: b x alt : 2
Mediana
editar
Mediana é o segmento de reta que une cada vértice do triângulo ao ponto médio do lado oposto. A mediana relativa à hipotenusa em um triângulo retângulo mede metade da hipotenusa.
O ponto de interseção das três medianas é o baricentro ou centro de gravidade do triângulo. O baricentro divide a mediana em dois segmentos. O segmento que une o vértice ao baricentro vale o dobro do segmento que une o baricentro ao lado oposto deste vértice. No triângulo Equilátero, as medianas, bissetrizes e alturas são coincidentes. No isósceles, apenas a que chegam ao lado diferente, no escaleno, nenhuma delas.
Bissetriz
editar
A bissetriz interna de um triângulo corresponde ao segmento de reta que parte de um vértice e vai até o segmento de reta, dividindo o ângulo do vértice em que partiu em dois ângulos congruentes.
Em um triângulo há três bissetrizes internas, sendo que o ponto de interseção delas chama-se incentro, que é o centro da circunferência inscrita no triângulo.
Já a bissetriz externa é o segmento da bissetriz de um ângulo externo situado entre o vértice e a interseção com o prolongamento do lado oposto.
Triângulo retângulo
editar- Como dito anteriormente, um triângulo retângulo é aquele no qual um dos ângulos internos é reto.
Catetos e Hipotenusa
editar- Em um triângulo retângulo, são chamados de catetos os lados perpendiculares entre si, ou seja, aqueles que formam o ângulo reto, e é chamado de hipotenusa o lado oposto ao ângulo reto.

- A altura relativa à hipotenusa é o segmento de reta que parte do ponto onde está o ângulo reto e vai perpendicularmente até a hipotenusa.
- As projeções dos catetos são as partes da hipotenusa divididas pela altura relativa.
Teorema de Pitágoras
editar
- Em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos.
- Seja a hipotenusa, sejam e catetos do mesmo triângulo:
Isso significa que, conhecendo as medidas de dois lados de um triângulo retângulo, pode-se calcular a medida do terceiro lado — propriedade única dos triângulos retângulos.
Demonstração do Teorema
editarPor semelhança
editar
Existem várias formas de demonstrar o Teorema de Pitágoras. Esta demonstração é baseada na proporcionalidade de dois triângulos semelhantes.
Seja um triângulo retângulo, com o ângulo reto localizado em , como mostrado na figura. Nós desenhamos o segmento de reta que passa por e é perpendicular a . O novo triângulo é semelhante ao nosso triângulo , pois ambos tem um ângulo reto (por definição de perpendicular), e eles compartilham o ângulo em , implicando que o terceiro ângulo terá a mesma medida em ambos. De forma análoga, o triângulo também é semelhante a . A semelhança leva a duas razões:
- e
Isto pode ser escrito como:
- e
Somando as duas igualdades, obtemos:
Em outras palavras, o Teorema de Pitágoras:
Por equivalência de polígonos
editarEsta demonstração se baseia na congruência de triângulos e na equivalência de área de quadriláteros.

Dado retângulo em e seja a altura relativa à hipotenusa, marcamos na semi-reta um ponto tal que (lembre que é a hipotenusa). Então construímos o retângulo (lembre que é a projeção de ).
Agora construímos . A semi-reta intercepta em um ponto , assim como em um ponto . Temos o paralelogramo .
Como e são paralelogramos de mesma base e mesma altura, ambos tem a mesma área.
Por definição de quadrado, segue que , e também é reto. Portanto, .
e são ambos suplementares de . Portanto, .
Segue pelo critério lado-ângulo-ângulo de congruência de triângulos que . Portanto, , e por extensão, .
Como e são paralelogramos de mesma base e mesma altura, ambos tem a mesma área. Ou seja, a área do quadrado sobre um cateto é igual à área do retângulo determinado pela projeção deste cateto e um segmento congruente à hipotenusa. Como a união do retângulo determinado por e com o retângulo determinado por e é igual ao quadrado sobre , segue que a soma das áreas dos quadrados sobre os catetos é igual a área do quadrado sobre a hipotenusa.
Q.E.D.
Aplicações do Teorema
editar- Com o teorema de Pitágoras, pode-se calcular o comprimento da hipotenusa de um triângulo conhecendo apenas o comprimento de cada cateto deste. Ou ainda, calcular o comprimento de um cateto conhecendo apenas a medida da hipotenusa e de outro cateto. O teorema de Pitágoras pode também ser usado para calcular o comprimento da diagonal de um retângulo conhecendo apenas os lados deste.
Exemplos
editar- Seja um triângulo retângulo no qual consista em um dos catetos o qual mede 3 metros de comprimento e consista em outro cateto o qual mede 4 metros de comprimento. Calcule o comprimento da hipotenusa .
- Resolução
- Dado o Teorema de Pitágoras, , tem-se que e , portanto:
- A hipotenusa do triângulo mede 5 metros.
- Um triângulo retângulo tem os lados , e , sendo que é um cateto e mede 1 centímetro de comprimento, enquanto é a hipotenusa e mede 2 centímetros. Calcule o comprimento do cateto
- Resolução
- Dado o Teorema de Pitágoras, , tem-se que e , portanto:
- O cateto mede centímetros de comprimento.
Triângulos retângulo notáveis
editarTriângulo 3_4_5
editar
Um "triângulo 3_4_5" é qualquer triângulo retângulo que tenha esta proporção de lados. Ou seja, um triângulo cujo um dos catetos tem o comprimento , outro cateto, o comprimento e a hipotenusa, ; tal que haja um número que:
|
|
|
|
A consciência desta proporção permite, a partir do comprimento de dois lados de um triângulo 3_4_5, inferir rapidamente o comprimento do terceiro lado. Por exemplo, sabendo que um triângulo tem um lado de 6 metros e outro de 8 metros, pode-se inferir corretamente que o outro lado tem 10 metros (onde n=2).
Triângulo 45º_45º_90º
editarO chamado "triângulo 45º_45º_90º" possui ângulos com essas medidas e a proporção entre seus lados é: . Ou seja, um triângulo retângulo e isóceles.
Triângulo 20º_70º_90º
editarO "triângulo 30º_60º_90º" possui ângulos com essas medidas e a proporção de seus lados é: .
Exercícios resolvidos
editarNa comédia antiga Diálogo dos mortos, do poeta satírico Luciano de Samósata, Hermes empilha as montanhas Ossa e Pelion sobre o Olimpo, na esperança de, a partir de um ponto de vista mais alto, poder mostrar toda a Terra para Caronte; para sua decepção, porém, ele só consegue ver ao oeste, parte da Itália, ao sul, até Creta, ao leste, até a Jônia e, ao norte, até o Danúbio.[1] Considerando a Terra esférica, que a visão corresponde a um raio tangente, que o ponto mais distante observado seja o ponto de tangência, que a soma da altura dos três montes seja 5 km e que a distância até o ponto de tangência seja 400 km, calcule qual foi o raio da Terra usado por Luciano.
Ver também
editar- Trigonometria
- Lei dos senos e dos cossenos
- Demonstração ilustrada do Teorema de Pitágoras na edição de Byrne dos Elementos de Euclides
Referências
editar- ↑ Luciano de Samósata, Diálogo dos mortos, Caronte
Esta página foi eleita pelos colaboradores como uma das melhores do Wikilivros. Para mais informações, consulte a página de votações.
Polígonos
editarPolígonos são figuras geométricas planas das formadas por segmentos de reta interligados entre si fechados (linha poligonal fechada).
Elementos dos polígonos
editarUm polígono possui os seguintes elementos:

- Arestas ou lados: cada um dos segmentos de reta que unem vértices consecutivos: , ,,,.
- Perímetro: soma das arestas (ou lados).
- Vértices: ponto de encontro (intersecção) de dois lados consecutivos: A, B, C, D, E.
- Altura: linha vertical que liga as duas extremidades do polígono.
- Diagonais: segmentos que unem dois vértices não consecutivos:,,,,.
- Ângulos internos: ângulos formados por dois lados consecutivos: ,,,,
- Ângulos externos: ângulos formados por um lado e pelo prolongamento do lado a ele consecutivo: ,,,,.
Classificação
editarOs polígonos são classificados:
Em termos dos ângulos
editarEm termos das medidas de seus ângulos, um polígono pode ser:
- Convexo: se possui todos os seus ângulos internos convexos — isto é, entre 0° e 180°; ou
- Côncavo: se possui um ângulo interno côncavo — superior a 180°.
Quanto ao número de lados
editarNão há restrições quanto ao número de lados n de um polígono desde que n ≥ 3. Embora apenas alguns possuam nomenclatura própria, segue uma tabela com alguns destes nomes:
| Lados | Nome | Lados | Nome | Lados | Nome |
|---|---|---|---|---|---|
| inexistente | 11 | Undecágono | ... | ||
| 25 | icosikaipentagono | ||||
| inexistente | 12 | Dodecágono | |||
| ... | |||||
| 3 | Triângulo | 13 | tridecágono | 30 | triacontágono |
| 4 | Quadrilátero | 14 | tetradecágono | 40 | tetracontágono |
| 5 | Pentágono | 15 | pentadecágono | 50 | pentacontágono |
| 6 | Hexágono | 16 | hexadecágono | 60 | hexacontágono |
| 7 | Heptágono | 17 | heptadecágono | 70 | heptacontágono |
| 8 | Octógono | 18 | octodecágono | 80 | octacontágono |
| 9 | Eneágono | 19 | eneadecágono | 90 | eneacontágono |
| 10 | Decágono | 20 | icoságono | 100 | hectágono |
A título de curiosidade, são mostrados a seguir os nomes de alguns polígonos cujos números de lados são potências de 10:
| Lados | Nome |
|---|---|
| 1000 | quilógono |
| 1.000.000 | megágono |
| 109 | gigágono |
Triângulos
editarVeja as páginas triângulos, pontos, linhas e círculos associados a um triângulo e triângulo retângulo.
Quadriláteros
editarQuadriláteros são as figuras geométricas planas formadas por quatro lados. Eles são classificados em seis tipos, dependendo da proporção entre seus lados e ângulos:

Quadrados
editarSão quadriláteros em que todos os ângulos são iguais (a 90°) e todos os lados têm a mesma medida. Portanto, todos os quadrados apresentam semelhança de ângulos e lados. Pelo fato de o quadrado possuir quatro lados l idênticos, o perímetro P pode ser facilmente deduzido por

Também, para todos os quadrados, pode-se deduzir através do teorema de Pitágoras a sua diagonal d, ora, pois, o quadrado é formado pela união de dois triângulos retângulos idênticos:
Conclui-se que a diagonal de qualquer quadrado é igual ao produto de seu lado por √2.

Retângulos
editarUm retângulo é um paralelogramo, cujos lados formam ângulos retos entre si e que, por isso, possui dois lados paralelos verticalmente e os outros dois paralelos horizontalmente. Todos os ângulos internos no retângulo são iguais a 90°, mas seus lados podem ser diferentes. Pode-se considerar o quadrado como um caso particular de um retângulo em que todos os lados têm o mesmo comprimento. O perímetro do retângulo, pode, então, ser deduzido por
Em que a e b são os lados do retângulo. Igual ao quadrado, a diagonal d do retângulo é dada pelo teorema de Pitágoras:
Losangos
editarSão quadriláteros em que todos os lados possuem a mesma medida, assim como o quadrado. Entretanto, dois de seus ângulos se diferem. Considerando que a figura ao lado é um losango, obrigatoriamente os ângulos A e C são iguais entre si. Os ângulos B e D também são iguais (mas não necessariamente iguais a A e C). O quadrado é um caso particular do losango. O perímetro é dado por:
Já suas diagonais podem ser calculadas de duas formas: pela lei dos cossenos ou pela regra do paralelogramo. Caso você queira encontrar a diagonal oposta a um certo ângulo, utiliza-se lei dos cossenos. No caso de se querer a diagonal adjacente (a que parte do ângulo), calcula-se usando a regra do paralelogramo. Por exemplo, considere um losango de lados b e c igual a 2, e descubra a medida da diagonal oposta a de um ângulo α de 60°. Pela lei dos cossenos:
Então (lembre-se que no losango todos os lados são iguais):
Paralelogramos
editar
São quadriláteros cujos pares de lados opostos são iguais e paralelos. Portanto, o perímetro do paralelogramo é dado da mesma forma que o de um retângulo. Além disso, seus ângulos opostos são idênticos (da mesma forma que o losango), e por isso, a forma de se calcular as diagonais de um paralelogramo é igual a de um losango. Todas as figuras explicadas anteriormente são casos especiais do paralelogramo. Por fim, a regra matemática que leva o nome desta figura diz que:
Em que a é uma semirreta que parte do ângulo α formando uma diagonal adjacente do paralelogramo. Observe a semelhança entre a regra do paralelogramo e a lei dos cossenos: o que muda é o sinal que antecede a expressão 2bc cos α. Exemplo: qual a diagonal adjacente do ângulo 60° de um paralelogramo, formado por lados iguais a 1 e 3?

Trapézios
editarSão quadriláteros que possuem dois lados paralelos (bases). Desta forma, diferentemente das figuras anteriores, seus ângulos são totalmente livres e independentes entre si. Os ângulos e as diagonais podem ser dados pela lei dos senos, lei dos cossenos ou pela regra do paralelogramo. As diagonais do trapézio x e y dão dadas por
Onde a é a base menor, c a base maior, e b e d os lados adjacentes à base. O perímetro é dado pela soma de todos os lados.
Fórmulas
editarÂngulos
editarPara que se determine a soma de todos os ângulos internos de um polígono convexo, aplica-se a seguinte fórmula:
Já a soma dos ângulos externos vale 360º.
Área
editarAbaixo estão as fórmulas para a área (A) de cada polígono (perceba que estas fórmulas podem ser incorporadas a outras propriedades dos polígonos, como altura [h], diagonal [d e D], perímetro, ângulos, etc). Considere B e b as bases dos polígonos, e l o lado do quadrado:
| Triângulo | |
| Quadrado | |
| Retângulo | |
| Losango | |
| Paralelogramo | |
| Trapézio |
Polígonos regulares
editar



Todo polígono regular possui seus n lados e os ângulos com medidas iguais. Como os ângulos internos e externos são iguais, obtém-se a medida de cada ângulo A (interno ou externo) por:
Alguns polígonos regulares têm nomes especiais: o triângulo regular é o triângulo equilátero, e o quadrilátero regular é o quadrado. Pelo fato de todos os polígonos regulares serem iguais entre si em ângulos, suas áreas, perímetros, diagonais e alturas podem ser sintetizadas em fórmulas em função de seus lados (ou outra propriedade que não seja o ângulo). Um método muito prático para tal feito é dividir o polígono regular em n triângulos idênticos. Exemplo: qual a fórmula para a área A do hexágono regular em função de seu lado l?
- Primeiramente, traçaremos os triângulos no hexágono:
- Calcularemos a soma dos ângulos internos deste polígono:
- Podemos agora calcular a medida de cada ângulo interno do hexágono regular:
- Portanto, os ângulos que formam cada triângulo são de 60° (perceba que cada ângulo de 120° forma dois triângulos). O hexágono é, portanto, formado por seis triângulos equiláteros idênticos. Sabemos que a área do triângulo equilátero é
- Então a área de seis destes triângulos é equivalente à área do polígono. Logo
Congruência
editarDois ângulos são congruentes se, sobrepostos um sobre o outro, todos os seus elementos coincidem. Nos paralelogramos, os lados paralelos são congruentes, e dois ângulos opostos pelo vértice são sempre congruentes. Num triângulo equilátero, todos os lados e ângulos são congruentes; nos triângulos isósceles, apenas os lados iguais e os ângulos da base são congruentes.
Semelhança
editarGeometria plana/Circunferência e círculo
editarAqui, será feito o estudo destas duas formas geométricas.
- Circunferência: A borda da figura geométrica. É a parte atingida pela tangente;
- Círculo: A parte interna da figura geométrica. É atingida, juntamente com a circunferência, pela secante.
Circunferência
editar
A circunferência é apenas a forma do círculo ou medida.
Como calcular a área de uma circunferência
A área de um círculo (figura delimitada por uma circunferência) é calculada multiplicando-se o quadrado do raio por Pi, constante matemática que tem o valor de, aproximadamente, 3,1416.
Ou seja : S (área) = Pi (3,1416) x R²
Assim, por exemplo, um círculo cujo raio seja de 10 cm terá como área s = 3,1416 x 10 = 314,16 cm quadrados.
Comprimento
editar
Círculo
editarÁrea
editar- Onde "A" é a área, "r" é o raio e (=3,14...) é uma constante.
Setores
editarCírculo circunscrito
editarCírculo inscrito
editarUma circunferência inscrita, é uma circunferência que esta dentro de um polígono regular.
|
Esta página é um esboço de geometria. Ampliando-a você ajudará a melhorar o Wikilivros. |
Construções geométricas usando régua e compasso
editarIntrodução
editar
Triângulo Eqüilátero
editarAbra o seu compasso em qualquer tamanho, trace um arco. Com a mesma abertura trace outro arco tendo como centro qualquer ponto do arco já traçado. Agora, ainda com o mesmo raio, trace um arco tendo como centro a intersecção do outro dois arcos anteriores. Ligue as três intersecções. Você tem agora um triângulo equilátero.
Mediatriz
editarQuadrado
editarTrace uma circunferência, trace um diâmetro em segunda, trace outro diâmetro perpendicular ao primeiro. Cada ponta das retas que formaram o diâmetro forma um ponto do quadrado, e depois é só unir esses pontos.
Pentágono
editarHexágono
editarBisecção do ângulo
editarExercícios
editar
|
Esta página é um esboço de geometria. Ampliando-a você ajudará a melhorar o Wikilivros. |
Áreas e volumes
editarÁrea do paralelogramo
editarTipos de paralelogramos
Área do retângulo
editarA área do retângulo é o produto de seu lado por sua altura. A área de quadrado é um caso particular da área do retângulo, assim como a figura quadrado é um caso particular da figura retângulo.
Área do losango
editar
Área do quadrado
editar- Seja a área do quadrado e seu lado:
Área do triângulo
editarA área do triângulo é o produto de sua base por sua altura dividido por dois.
Assim teremos de um modo geral =
b = medida da base AB
h= medida da altura relativa do lado AB
Obs: o Teorema de Heron permite calcular a área de um triângulo qualquer a partir das dimensões dos seus lados
Área do trapézio
editarA área do trapézio é o produto de sua altura pela média aritmética das bases (denotadas por B e b).
Área do círculo
editar
Geometria espacial
editar- Figuras geométricas espaciais - retas e planos no espaço, ângulos diédricos e poliédricos, poliedros convexos, poliedros regulares.
- Posições relativas de retas e planos - paralelismo e perpendicularismo no espaço, retas reversas.
- Prismas, Pirâmides, Cilindros, Cones e seus respectivos troncos - cálculo de áreas e volumes.
- Esfera e superfície esférica - cálculo de áreas e volumes.
- Semelhança de figuras planas ou espaciais - razão entre comprimentos, áreas e volumes.
|
Esta página é um esboço de geometria. Ampliando-a você ajudará a melhorar o Wikilivros. |
Pirâmides
editarPirâmide Regular
editarPirâmide regular é uma pirâmide cuja base é um polígono regular e projeção ortogonal do vértice sobre o plano da base é o centro da base.
Fórmulas
editar- Área da base (): área de um poligono.
- Área lateral (): soma das áreas das faces laterais.
- Área total:
- Volume:
- área das faces laterais base x h (altura) dividido por 2 .
|
Esta página é um esboço de geometria. Ampliando-a você ajudará a melhorar o Wikilivros. |
Geometria analítica
editar- Vetores - O que são vetores?
- Coordenadas cartesianas - Localização de pontos numa reta e num plano usando coordenadas cartesianas, distância entre dois pontos, o uso de coordenadas cartesianas para a solução de problemas geométricos simples na reta e no plano.
- Cálculo com vetores - Soma e subtração de vetores, multiplicação de um real por um vetor, norma e módulos de vetores, produto escalar de vetores.
- Estudo da reta em geometria analítica plana - Equação da reta na forma normal, coeficiente angular, condições de paralelismo e perpendicularismo de retas, equações e inequações de primeiro grau em duas variáveis, distância de um ponto a uma reta.
- Estudo da circunferência em geometria analítica - Equação, intersecção de retas e circunferências, retas tangentes a circunferências, intersecção e tangência de circunferências.
- Representação analítica de lugares geométricos, Definição e representação de cônicas, Equação reduzida de uma cônica, Intersecção de retas e cônicas.
Ver também
editar
|
Esta página é um esboço de geometria. Ampliando-a você ajudará a melhorar o Wikilivros. |
Estatística
editarA Estatística é um ramo da Matemática que tem por objetivo obter, organizar e analisar dados, determinar as correlações que apresentem, tirando delas suas consequências para descrição e explicação do que passou e previsão e organização do futuro.
A Estatística é também uma ciência e prática de desenvolvimento de conhecimento humano através do uso de dados empíricos. Baseia-se na teoria estatística, um ramo da matemática aplicada. Na teoria estatística, a aleatoriedade e incerteza são modeladas pela teoria da probabilidade. Algumas práticas estatísticas incluem, por exemplo, o planejamento, a sumariação e a interpretação de observações. Porque o objetivo da estatística é a produção da "melhor" informação possível a partir dos dados disponíveis, alguns autores sugerem que a estatística é um ramo da teoria da decisão.
Introdução
editarEncontrar padrões é algo que a humanidade faz a todo momento. Nossa sobrevivência depende da nossa capacidade de prever eventos. Para entender esses eventos criamos ferramentas como a ciência, a matemática, e a filosofia.
Unindo duas áreas, a matemática e a ciência, um dos resultados foi a estatística. Uma forma de matemática aplicada, muito útil para descrever sistemas complexos, que não podem ser isolados e dessecados. A natureza está repleta de sistemas assim, o comportamento de populações de borboletas ou de seres humanos pode ser visto de entendido usando princípios estatísticos.
A etapa inicial de entender o objeto ou sistema, é feita pela estatística descritiva, responsável por organizar e sumarizar dados. Já a estatística indutiva ou inferencial trabalha para encontrar padrões, leis que descrevam o comportamento de um sistema.
Estatística Dedutiva ou Descritiva
editarEstatística Indutiva ou Inferêncial
editarMedidas de Posição
editarMedidas de Tendência Central
editarMédia
editarMédia Aritmética
editarA média aritmética é o cálculo feito em um cálculo de adição e divisão pela porção de parcelas.
Exemplo:
O cálculo se inicia com a adição e depois passa-se à divisão.
Podemos também considerar a seguinte fórmula: μ=
Onde:
∑ = somatório;
xi= cada elemento x de 1 até n; e
n= número de elementos do conjunto de dados.
Média Geométrica
editarMédia Harmônica
editarMediana
editarÉ o valor (elemento) que ocupa posiçao central em uma serie estatistica, deixando 50% (metade) dos valores á´sua esquerda (menores) e 50% á sua direita (maiores). EX; - Calcule a mediana para as series estatisticas: a)- X: 11, 7,7,9,8,10,13. X: 7,7,8,9,10,11,13. 50% dos valores sao menores ou iguais a 9 e 50% dos valores são maiores a 9.
Se o número de observações (N) for impar a mediana ocupa posição central.
Moda
editarA moda de um conjunto de valores é definida como o valor que ocorre com maior freqüência. Referências comuns à moda incluem expressões como valor dominante, valor que ocorre o maior número de vezes, valor que predomina num conjunto, valor modal, valor mais comum, etc.
Não é imperativa, mas a ordenação dos dados facilita a identificação do valor mais freqüente.
Se num conjunto de observações não se repetir nenhuma observação, ele não tem moda e é considerado amodal.
Se o conjunto tiver apenas um único valor que se repete em frequência máxima, ele tem apenas uma moda e é considerado unimodal.
Se o conjunto tiver dois valores que se repetem em igual frequencia máxima, ele tem duas modas e é bimodal.
E, se um conjunto tiver tres ou mais valores com mesma frequencia máxima, ele tem tres ou mais modas e é considerado Multimodal ou Polimodal.
Moda Czuber
editarModa King
editarModa Karl Pearson
editarMedidas Separatrizes
editarÉ um tipo de separatriz que divide a série estatística em quatro partes iguais de 25% cada - e possui três divisórias, que são Q1, Q2 e Q3, significando respectivamente, 1º quartil ou quartil inferior, 2º quartil ou quartil médio e 3º quartil ou quartil superior.
Quartil
editarÉ a divisão do meu conjunto de observações em quatro partes iguais.
Temos então três quartis: Q1, Q2 e Q3, onde Q2 coincide com a mediana.
ex.: 2 4 6 8 10 12 14.
A mediana é 8, portanto meu Q2 também será o 8: 2 4 6 8 10 12 14.
Seguindo esse conceito, teremos: Q1 = 4 e Q3 = 12.
Onde: 2 4 6 8 10 12 14
Decil
editarCentil ou Percentil
editarMedidas de Dispersão
editarAbsoluta
editarDesvio Padrão
editarDesvio Padrão é o valor que varia para mais ou para menos. Para encontrar o Desvio Padrão é necessário encontrar raiz quadrada da Variância. Para encontrar a Variância é necessário encontrar os valores da Média, Desvio e Quadrado dos Desvios. A soma do quadrado dos desvios dividida pela soma de todos os itens, resulta em um número X chamado Variância. Deve-se achar a raiz quadrada desse número X para então obter o valor do Desvio Padrão.
Desvio Quadrático (Variância)
editarDesvio Quartílico
editarDesvio Médio
editarRelativa
editarVariância Relativa
editarCoeficiente de Variação
editarCoeficiente de Variação é a divisão do Desvio Padrão pela média. Para encontrar o Desvio Padrão, deve calcular a raiz quadrada da Variância, que por sua vez é a média dos quadrados menos o quadrado da média.
Medidas de Curtose
editarVer também
editar- Probabilidade e Estatística - livro com conteúdo mais avançado
|
Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros. |
Cálculo
editarO estudo do Cálculo envolve três conceitos:
- limite
- derivada
- integral
Embora atualmente os livros texto os apresentem para o aluno nesta ordem, eles foram definidos e usados na ordem inversa. A princípio só havia o conceito de integral. Para formalizar o conceito foi definida e usada a idéia de derivada. Finalmente para formalizar ambos os conceitos de derivada e integral, foi definido o limite.
Quando se estuda cálculo, limite é o que tem menos aplicações práticas. Derivadas um pouco mais e integral tem muitas aplicações interessantes. Então, se você estiver achando o começo do estudo meio chato, não desanime. Quando chegar em derivada fica um pouco melhor e quando chegar em integral fica muito mais gostoso.
|
Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros. |
Glossário
editarO seguinte glossário contém palavras usadas neste livro, em suas diferentes acepções quando for o caso. Procurou-se especificar também palavras sinônimas e com grafias diferentes.
A
editarÁlgebra (algebra). Parte da matemática que não trata especificamente com geometria. Esta é uma definição antiga. Hoje a álgebra pode ser dividida em clássica e moderna. A álgebra clássica é a parte que trata de manipulação simbólica e da solução de equações algébricas. A álgebra moderna ou abstrata lida com um ramo da matemática conhecido como estruturas discretas (corpos, grupos, anéis, etc.).
Álgebra de Boole (Boolean algebra). Tanto na Matemática quanto na Ciência Computacional uma álgebra Booleana ou de Boole ou ainda um reticulado (lattice) Booleano é uma estrutura algébrica que lida com as operações lógicas E, OU e NÃO de mesma forma que lida com as operações sobre conjuntos correspondentes UNIÃO, INTERSECÇÃO e COMPLEMENTAÇÃO. Esta estrutura foi nomeada em homenagem ao matemático Inglês George Boole. A álgebra Booleana é uma tentativa de se utilizar técnicas algébricas para lidar com expressões do cálculo proposicional.
Algoritmo (algorithm). Um algoritmo é um conjunto definido de operações e passos ou procedimentos que objetivam levar a um particular resultado. Por exemplo, com algumas exceções, os programas computacionais, as fórmulas matemáticas e (de forma ideal) receitas médicas e culinárias são algoritmos.
Análise (analysis). Parte da matemática que lida com a aproximação de objetos matemáticos (como número e funções) por outros que são mais fáceis de entender e manejar.
Análise funcional (functional analysis). Parte da matemática que estuda espaços vetoriais de infinitas dimensões e bijeções entre eles. Os elementos destes espaços são muitas vezes funções, como, por exemplo, o espaço das funções contínuas sobre um intervalo.
Análise harmônica (harmonic analysis.) Veja teoria do potencial.
Anel (ring). É um conjunto munido de duas operações (normalmente denominadas de adição e multiplicação) que satisfazem certas propriedades (ou axiomas). Alguns anéis mais conhecidos são: dos reais, dos números complexos, dos polinômios, das matrizes. Muitos anéis são associativos, mas alguns podem não ser como os anéis de Lie.
Aproximação Diofantina (Diophantine approximation). Uma aproximação Diofantina é aproximar um número real através de um racional (razão entre inteiros).
Assíntota (assyntota). Reta cuja distância em relação a uma curva diminui indefinidamente sem nunca cortar a curva.
Axioma (axioma). Proposição que se aceita verdadeira sem demonstração.
B
editarBijeção-Relação onde cada elemento corresponde um e somente um elemento
C
editar- Conjunto
- Conceito primitivo: reunião de elementos (veja Conjuntos).
D
editar- Diferença (conjuntos)
- Operação envolvendo conjuntos que consiste em criar um novo conjunto (o conjunto diferença) contendo os elementos que estão contidos num conjunto, mas não estão contidos em outro.
E
editarF
editarG
editarH
editarI
editar- Intersecção
- Operação envolvendo (conjuntos) que consiste em criar um novo conjunto (o Conjunto intersecção) contendo os elementos que estão contidos simultâneamente em todos os conjuntos interseccionados.
J
editarK
editarL
editarM
editar- Matriz
- Elemento matemático formado por linhas e colunas, onde cada linha e cada coluna é um par ordenado.
N
editarO
editarP
editar- Par ordenado
- Par de elementos em que a ordem dos mesmo é fundamental; indicado por (a,b), sendo a e b os elementos ou coordenadas.
- Ponto matemático
- Um ponto é uma noção primitiva pela qual outros conceitos são definidos. Um ponto determina uma posição no espaço. Na Geometria, pontos não possuem volume, área, comprimento ou qualquer dimensão semelhante. Assim, um ponto é um objeto de dimensão 0 (zero). Um ponto também pode ser definido como uma esfera de diâmetro zero.
Q
editarR
editarS
editar- Subconjunto
- Conjunto contido em outro conjunto.
T
editarU
editar- União
- Operação envolvendo conjuntos que consite em criar um novo conjunto (o conjunto união) contendo todos os elementos dos conjuntos unidos, sem repetição.
- Universo
- Na teoria dos conjuntos, representa o conjunto que contém todos os subconjuntos passíveis de estudo, em determinado problema.
V
editarW
editarX
editarY
editarZ
editar|
Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros. |
Referências
editarLinks
editar- Matemática 1ª a 4ª série do fundamental
- Matemática Divertida
- Matemática do Científico e do Vestibular
- Matemática Essencial - Ensino: Fundamental, Médio e Superior
- Matemática - Wikipédia
- Apostilas do estágio da Olimpíada Brasileira de Matemática das Escolas Públicas (OBMEP)
Livros
editar- Dante, Luiz Roberto. Matemática: contexto e aplicações. Ensino Médio. Ática, 2000. 1 e 2 v.
- Goulart, Márcio Cintra. Matemática no ensino médio. Scipione, 1999. 1 e 2 v.
- Iezzi, Gelson, Dolce, Osvaldo, Machado, Antônio. Matemática e realidade. Atual, 1997. ISBN 857056788X































































































































































































![{\displaystyle 8^{{2} \over {3}}={\sqrt[{3}]{8}}^{2}={\sqrt[{3}]{64}}={4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc938620b68fb148bd16bb60dca454d97b3f4b6b)















![{\displaystyle {\sqrt[{n}]{x^{a}y^{b}z^{c}...}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f95bfaeeba70e150b4c0deebede65bfed52322d)















![{\displaystyle ]-\infty \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3631aa1a662e202102454cecace9992ea1dccec5)
![{\displaystyle ]a\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e12e8e3e0bbd8ae37eba339e3f02094ccc78b9)



![{\displaystyle b]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f13dcb677c27f083ad1faf4f3098491126f33b1)
![{\displaystyle ]-\infty ,0]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff9bb6365bdc0608883332b569943c0eac6b9838)

![{\displaystyle {\sqrt[{3}]{11}},{\sqrt {5}},2{\sqrt {2}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9208c53ed4f10692dd82202b6b4519d43ddc211d)
![{\displaystyle {\sqrt[{3}]{{\frac {x}{y}}{\sqrt[{4}]{\frac {x^{2}}{y}}}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc9ec5f02fb85076774695d085d2a115c4563cb4)
![{\displaystyle {\sqrt[{4}]{\frac {36}{125}}}{\sqrt[{3}]{\frac {5}{4}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d160b650dacb1f926ab2c3a6521643287a3f390)
![{\displaystyle {\sqrt[{6}]{x^{2}y}}{\sqrt[{4}]{x^{3}y^{2}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b34bc1ff07f6a9b7d3d1e34df07cf8c51efb3f7)




![{\displaystyle {\sqrt[{3}]{\frac {4^{2}}{9^{4}}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d547c528583c3c205f760109cb01cc5aa4fc37f7)
![{\displaystyle {\sqrt[{4}]{\frac {x^{6}.y^{9}}{z^{7}}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1749950535738833be91ee2b98dd4266a48beb0)



![{\displaystyle {\frac {\sqrt[{5}]{8}}{\sqrt[{5}]{4}}}=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c42f36a462afc4fd63e0cb340046e6dd6159c8ad)
![{\displaystyle {\frac {100}{{\sqrt[{3}]{2}}{\sqrt[{4}]{5}}}}=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56b10096a5884b1e5d3e2c2d85d7b1f6d1fc9c21)

![{\displaystyle {\frac {{\sqrt[{3}]{4}}+{\sqrt[{3}]{9}}}{{\sqrt[{3}]{2}}+{\sqrt[{3}]{3}}}}=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4fe019ce04a9413a01e7165d282b3a7db9b9c91)

![{\displaystyle {\sqrt[{3}]{x{\sqrt[{3}]{x{\sqrt[{3}]{x}}}}}}=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c69d07d7ac3e57f566de4ee699bf270915adabf2)
![{\displaystyle {\sqrt[{4}]{x^{3}{\sqrt[{3}]{x^{2}{\sqrt {x}}}}}}=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0fd4fc5ed763429e83e6a78bb4ce17da3936ca5)
![{\displaystyle {\sqrt[{10}]{x^{3}}}{\sqrt[{6}]{x^{5}}}=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/967eb0881cfef8b57ce3e1618b4565f2608ed638)
![{\displaystyle {\frac {\sqrt[{5}]{8}}{\sqrt[{3}]{4}}}=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/556eb96fb411c4183a446dbdafebf441c486a5db)
![{\displaystyle {\frac {125}{{\sqrt {5}}{\sqrt[{3}]{25}}}}=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6c775f274c01f62da5a285c0a78750c7582ca7e)
![{\displaystyle {\sqrt[{3}]{\frac {x^{4}\ y^{2}}{2\ z}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c68f5d8d8a513f46826eecac85c422cef8f98484)
![{\displaystyle {\sqrt[{3}]{\frac {x^{3}\ x\ y^{2}\ 2^{2}\ z^{2}}{2^{3}\ z^{3}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71175ca1068e18d758b1353adf8ae11647869915)
![{\displaystyle {\sqrt[{3}]{\frac {x^{3}}{2^{3}\ z^{3}}}}{\sqrt[{3}]{x\ 2^{2}\ y^{2}\ z^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fb2763d944fdccd180d19887941ac4face45c23)
![{\displaystyle {\frac {x}{2\ z}}{\sqrt[{3}]{2^{2}\ x\ y^{2}\ z^{2}}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe90479f96a7bf9b8305d79dcada2edc33c212e3)

![{\displaystyle {\sqrt[{5}]{\frac {64}{81}}}=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0568519a42f821120758206e6a00cc09276e8b1c)

![{\displaystyle {\sqrt[{15}]{x^{32}\ y^{83}\ z^{41}}}=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9fa9333fa949ab0f49643889eea3938affb8e75)









![{\displaystyle {\frac {1}{\sqrt[{3}]{2}}}+{\frac {1}{\sqrt[{3}]{4}}}-{\frac {1}{\sqrt[{3}]{16}}}=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f181c890a93a10f98b21a6389238678b75a0770)


![{\displaystyle ({\sqrt[{3}]{9}}-{\sqrt[{3}]{3}})^{2}=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f36d173457426711eafed96bfc2908e855ca550b)




























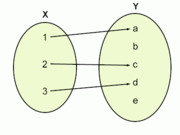



















![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


![{\displaystyle ]-\infty ,+\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fd2fe9ef14b0a4d8f00a13170d3c739302121b8)





































































































































![{\displaystyle \log _{a}b=c\iff a^{c}=b\iff {\sqrt[{c}]{b}}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcaaadd1b9370e43f794f79974ef4265fa3eeed6)

![{\displaystyle {\sqrt[{3}]{8}}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f378331b0d609846c021c1a0bbff0a4fc1755c3)










































































































































































































































































![{\displaystyle \mathrm {sen} \,\left(a+b\right)=\cos \left[{\frac {\pi }{2}}-\left(a+b\right)\right]=\cos \left[\left({\frac {\pi }{2}}-a\right)-b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0816e1dd2a297cfb5d28dab327714734a890da1)







































![{\displaystyle \cos \left(a-b\right)=\cos \left[a+\left(-b\right)\right]\;\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/025272648f7390cf4e3d1adad5add5a6c558d1aa)



![{\displaystyle \mathrm {sen} \,\left(a-b\right)=\mathrm {sen} \,\left[a+\left(-b\right)\right]=\mathrm {sen} \,a\cdot \cos \left(-b\right)+\mathrm {sen} \,\left(-b\right)\cdot \cos a\;\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee9609d266adb1eb06767bb9f997d1ba70a46b4b)

![{\displaystyle \tan \left(a-b\right)=\tan \left[a+\left(-b\right)\right]={\frac {\tan a+\tan \left(-b\right)}{1-\tan a\cdot \tan \left(-b\right)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36b2c317c03ad279d7bc689e53c3c5d511474b98)


![{\displaystyle \cot \left(a-b\right)=\cot \left[a+\left(-b\right)\right]={\frac {\cot a\cdot \cot \left(-b\right)-1}{\cot a+\cot \left(-b\right)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/563cf30ca50270ab92ad566f1fa339e3513d3c38)


















































































































![{\displaystyle {\begin{matrix}x=\alpha +2k\pi \\x=\pi -\alpha +2k\pi \\\alpha \in \left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52d8cd8bb4ea91ec7ad03034ffcdd43109759198)















































































































![{\displaystyle {\frac {a+b}{a-b}}={\frac {\tan[{\frac {1}{2}}({\widehat {A}}+{\widehat {B}})]}{\tan[{\frac {1}{2}}({\widehat {A}}-{\widehat {B}})]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99733869a4fc613c1e3e67384da4491ddc62080a)
![{\displaystyle {\frac {a+c}{a-c}}={\frac {\tan[{\frac {1}{2}}({\widehat {A}}+{\widehat {C}})]}{\tan[{\frac {1}{2}}({\widehat {A}}-{\widehat {C}})]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/842c1df3b4a8c76baa0f2fb405289e75b9ecccc2)
![{\displaystyle {\frac {b+c}{b-c}}={\frac {\tan[{\frac {1}{2}}({\widehat {B}}+{\widehat {C}})]}{\tan[{\frac {1}{2}}({\widehat {B}}-{\widehat {C}})]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03adc00954bb42600ec2f5b2d2c4c23ecf32d23e)




![{\displaystyle \Rightarrow {\frac {a+b}{a-b}}={\frac {\tan[{\frac {1}{2}}({\widehat {A}}+{\widehat {B}})]}{\tan[{\frac {1}{2}}({\widehat {A}}-{\widehat {B}})]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b580e2cd91f17569311450f2622a94ad82c0163)





































![{\displaystyle (n+8)^{2}-1=[(n+8)+1].[(n+8)-1]=[n+8+1].[n+8-1]=[n+9].[n+7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea8a3c7d36506c4c865e04bcc0dd32d396969f30)















![{\displaystyle {\sqrt[{3}]{a^{3}}}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4738d5cc892504d2cf95f68df45cf91314f0eb2c)
![{\displaystyle {\sqrt[{3}]{b^{3}}}=b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b38b79adad4d50918af60283a5b7ab4620b98a03)














![{\displaystyle {\frac {x^{6}}{64}}-{\frac {y^{6}}{729}}=\left({\frac {x^{3}}{8}}-{\frac {y^{3}}{27}}\right).\left({\frac {x^{3}}{8}}+{\frac {y^{3}}{27}}\right)=\left[\left({\frac {x}{2}}-{\frac {y}{3}}\right).\left({\frac {x^{2}}{4}}+{\frac {xy}{6}}+{\frac {y^{2}}{9}}\right)\right].\left[\left({\frac {x}{2}}+{\frac {y}{3}}\right).\left({\frac {x^{2}}{4}}-{\frac {xy}{6}}+{\frac {y^{2}}{9}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87eac5dd1f7ef5bddd493b6b52fa6e5d88a1244b)

























































![{\displaystyle {\sqrt[{}]{m^{2}}}=m}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67c226c3b35dfd8457ab45017b8980d0de74a851)
![{\displaystyle {\sqrt[{}]{25}}=5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f47bfc6f13f26f83042f2860c59ef3f1b01195e0)




















![{\displaystyle a\left[\left(x+{\frac {b}{2a}}\right)^{2}-\left({\frac {b^{2}}{4a^{2}}}-{\frac {c}{a}}\right)\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2dc99224629fbf2c6dc767b56ce37238bd786cb)
![{\displaystyle a\left[\left(x+{\frac {b}{2a}}\right)^{2}-\left({\frac {b^{2}-4ac}{4a^{2}}}\right)\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa6f9d5c1ef129c96357f2fb44b7857ea68f6de4)
![{\displaystyle a\left[\left(x+{\frac {b}{2a}}+{\frac {\sqrt {b^{2}-4ac}}{2a}}\right)\left(x+{\frac {b}{2a}}-{\frac {\sqrt {b^{2}-4ac}}{2a}}\right)\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5cd278aea93aa5bfa7889be2d7c7ba7c13db740)


![{\displaystyle a\left[\left(x+{\frac {b+{\sqrt {\Delta }}}{2a}}\right)\left(x+{\frac {b-{\sqrt {\Delta }}}{2a}}\right)\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8103a2a6ebfdb6540dc35c38c8339148f4d67fd0)


![{\displaystyle a\left\{x-x_{1}\right\}\left[x-x_{2}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9664a531d4bf63f008242519f88c5870b8f6813)

































![{\displaystyle {\sqrt {4\times 9}}={\sqrt[{}]{36}}=6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1738716d2322818517b5fb388eb2b8751c4d772e)






















































































































![{\displaystyle =-2{\bigg [}(-1)\cdot (-1)-3\cdot 2{\bigg ]}+1{\bigg [}(-2)\cdot (-1)-(-3)\cdot 2{\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b990bedcc088e097c6a5693d182a2665af3485c)